
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)求过点![]() 且与抛物线
且与抛物线![]() 的准线相切的圆的方程.
的准线相切的圆的方程.
科目:高中数学 来源: 题型:
【题目】某乡镇为了发展旅游行业,决定加强宣传,据统计,广告支出费![]() 与旅游收入
与旅游收入![]() (单位:万元)之间有如下表对应数据:
(单位:万元)之间有如下表对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求旅游收入![]() 对广告支出费
对广告支出费![]() 的线性回归方程
的线性回归方程![]() ,若广告支出费
,若广告支出费![]() 万元,预测旅游收入;
万元,预测旅游收入;
(2)在已有的五组数据中任意抽取两组,根据(1)中的线性回归方程,求至少有一组数据,其预测值与实际值之差的绝对值不超过![]() 的概率.(参考公式:
的概率.(参考公式: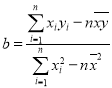 ,
,![]() ,其中
,其中![]() 为样本平均值,参考数据:
为样本平均值,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:![]() ;
;![]() ;
;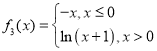 ;
;![]() .则其中是“偏对称函数”的函数个数为( )
.则其中是“偏对称函数”的函数个数为( )
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com