
【题目】已知函数![]() 的图像过点
的图像过点![]() ,且在
,且在![]() 处取得极值.
处取得极值.
(1)若对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)当![]() ,试讨论函数
,试讨论函数![]() 的零点个数.
的零点个数.
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为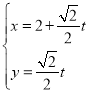 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
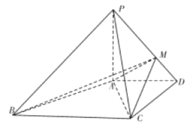
(1)取![]() 中点
中点![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
(3)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成角,如果不存在,请说明理由.
所成角,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路![]() 进行分流,已知穿城公路
进行分流,已知穿城公路![]() 自西向东到达城市中心
自西向东到达城市中心![]() 后转向
后转向![]() 方向,已知
方向,已知![]() ,现准备修建一条城市高架道路
,现准备修建一条城市高架道路![]() ,
,![]() 在
在![]() 上设一出入口
上设一出入口![]() ,在
,在![]() 上设一出口
上设一出口![]() ,假设高架道路
,假设高架道路![]() 在
在![]() 部分为直线段,且要求市中心
部分为直线段,且要求市中心![]() 与
与![]() 的距离为
的距离为![]() .
.
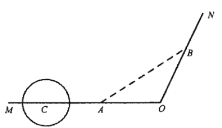
(1)若![]() ,求两站点
,求两站点![]() 之间的距离;
之间的距离;
(2)公路![]() 段上距离市中心
段上距离市中心![]()
![]() 处有一古建筑群
处有一古建筑群![]() ,为保护古建筑群,设立一个以
,为保护古建筑群,设立一个以![]() 为圆心,
为圆心,![]() 为半径的圆形保护区.因考虑未来道路
为半径的圆形保护区.因考虑未来道路![]() 的扩建,则如何在古建筑群和市中心
的扩建,则如何在古建筑群和市中心![]() 之间设计出入口
之间设计出入口![]() ,才能使高架道路及其延伸段不经过保护区?
,才能使高架道路及其延伸段不经过保护区?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,且离心率为
,且离心率为![]() ,点
,点![]() 为椭圆上的动点,
为椭圆上的动点,![]() 面积最大值为
面积最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)![]() 是椭圆
是椭圆![]() 上的动点,且直线
上的动点,且直线![]() 经过定点
经过定点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 若存在,请求出定点
若存在,请求出定点![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),过椭圆的左顶点和上顶点的直线
在第一象限),过椭圆的左顶点和上顶点的直线![]() 与直线
与直线![]() 交于
交于![]() 点,且满足
点,且满足![]() ,设
,设![]() 为坐标原点,若
为坐标原点,若![]() ,
,![]() ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据: ![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com