
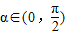 ,使
,使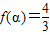 ;②存在
;②存在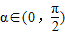 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点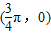 对称.
对称. 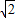 sin(x+
sin(x+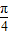 ),确定函数的值域,判断①的错误;找出特殊值判断②;函数的对称轴判断③的正误;
),确定函数的值域,判断①的错误;找出特殊值判断②;函数的对称轴判断③的正误;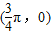 代入函数成立,说明④正确.
代入函数成立,说明④正确.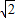 sin(x+
sin(x+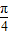 ),
),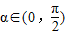 时 y∈(1,
时 y∈(1,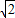 ],因为
],因为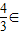 (1,
(1,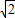 ],所以①正确.
],所以①正确.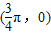 对称,当x=
对称,当x=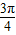 时f(
时f(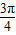 )=0,满足题意,所以正确.
)=0,满足题意,所以正确.

科目:高中数学 来源: 题型:
| π |
| 2 |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| π |
| 2 |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| π |
| 2 |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年高三(上)数学寒假作业(理科)(解析版) 题型:填空题
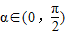 ,使
,使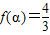 ;②存在
;②存在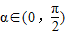 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点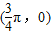 对称.
对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com