
【题目】设函数f(x)=x3+bx2+cx(x∈R),已知g(x)=f(x)﹣f′(x)是奇函数
(1)求b、c的值.
(2)求g(x)的单调区间与极值.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据g(x)=f(x)﹣f'(x)是奇函数,且f'(x)=3x2+2bx+c能够求出b与c的值;
(2)对g(x)进行求导,g'(x)>0时的x的取值区间为单调递增区间,g'(x)<0时的x的取值区间为单调递减区间.g'(x)=0时的x函数g(x)取到极值.
(1)∵f(x)=x3+bx2+cx,∴f'(x)=3x2+2bx+c.
从而g(x)=f(x)﹣f'(x)=x3+bx2+cx﹣(3x2+2bx+c)=x3+(b﹣3)x2+(c﹣2b)x﹣c
是一个奇函数,所以g(0)=0得c=0,由奇函数定义得b=3;
(2)由(Ⅰ)知g(x)=x3﹣6x,从而g'(x)=3x2﹣6,
当g'(x)>0时,x<﹣![]() 或x>
或x>![]() ,
,
当g'(x)<0时,﹣![]() <x<
<x<![]() ,
,
由此可知,g(x)的单调递增区间为(﹣![]() ),(
),(![]() ,+∞);单调递减区间为(﹣
,+∞);单调递减区间为(﹣![]() ,
,![]() );
);
g(x)在x=﹣![]() 时取得极大值,极大值为4
时取得极大值,极大值为4![]() ,
,
g(x)在x=![]() 时取得极小值,极小值为4
时取得极小值,极小值为4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
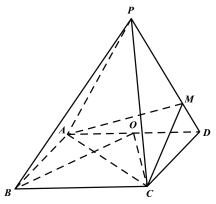
【题目】如图,四棱锥P-ABCD的底面是平行四边形,PD⊥AB,O是AD的中点,BO=CO.
(1)求证:AB⊥平面PAD;
(2)若AD=2AB=4, PA=PD,点M在侧棱PD上,且PD=3MD,二面角P-BC-D的大小为![]() ,求直线BP与平面MAC所成角的正弦值.
,求直线BP与平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区农产品近几年的产量统计如下表:

为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表:
得到下表:

(1)根据表中数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若近几年该农产品每万吨的价格![]() (万元)与年产量
(万元)与年产量![]() (万吨)满足
(万吨)满足![]() ,且每年该农产品都能售完,当年产量
,且每年该农产品都能售完,当年产量![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分別为:
的斜率和截距的最小二乘估计分別为: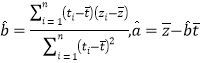 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.设命题![]() :
:![]() ,
,![]() .则
.则![]() :
:![]() ,
,![]() ;
;
B.若![]() ,
,![]() ,则
,则![]() ;
;
C.若![]() 是定义在
是定义在![]() 上的减函数,则“
上的减函数,则“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
D.若![]() ,
,![]() ,
,![]() (
(![]() )是全不为0的实数,则“
)是全不为0的实数,则“![]() ”是“不等式
”是“不等式![]() 和
和![]() 解集相等”的充分不必要条件.
解集相等”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
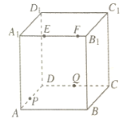
【题目】如图,正方体![]() 的棱长为4,动点E,F在棱
的棱长为4,动点E,F在棱![]() 上,动点P,Q分别在棱AD,CD上。若
上,动点P,Q分别在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),则四面体PEFQ的体积
大于零),则四面体PEFQ的体积
A.与![]() 都有关B.与m有关,与
都有关B.与m有关,与![]() 无关
无关
C.与p有关,与![]() 无关D.与π有关,与
无关D.与π有关,与![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在实数集![]() 上的函数
上的函数![]() ,
,![]() 恒不为0,若存在不等于1的正常数
恒不为0,若存在不等于1的正常数![]() ,对于任意实数
,对于任意实数![]() ,等式
,等式![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 函数.
函数.
(1)若函数![]() 为
为![]() 函数,求出
函数,求出![]() 的值;
的值;
(2)设![]() ,其中
,其中![]() 为自然对数的底数,函数
为自然对数的底数,函数![]() .
.
①比较![]() 与
与![]() 的大小;
的大小;
②判断函数![]() 是否为
是否为![]() 函数,若是,请证明;若不是,试说明理由.
函数,若是,请证明;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
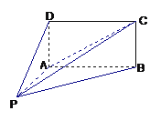
(I)平面PAD与平面PAB是否垂直?并说明理由;
(II)求平面PCD与平面ABCD所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足下列条件:①f(x)不恒为0;②对任意的正实数x和任意的实数y都有f(xy)=yf(x).
(1)求证:方程f(x)=0有且仅有一个实数根;
(2)设a为大于1的常数,且f(a)>0,试判断f(x)的单调性,并予以证明;
(3)若a>b>c>1,且![]() ,求证:f(a)f(c)<[f(b)]2.
,求证:f(a)f(c)<[f(b)]2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com