练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知公差大于零的等差数列{an}的前n项和为Sn,且满足:a3·a4=117,a2+a5=22.
    (1)求数列{an}的通项公式an.
    (2)若数列{bn}是等差数列,且bn=,求非零常数c.
    (1) n= 4n-3          (2)c=-
    (1)由得
    解得或
    ∵公差d>0,∴a3=9,a4=13,∴d=4.
    ∴an=a3+(n-3)d=9+(n-3)·4=4n-3.
    (2)Sn===2n2-n.
    bn==.
    ∵{bn}是等差数列,
    ∴b1+b3=2b2.
    ∴+=2·,
    ∴2c2+c=0.
    ∵c≠0,∴c=-,经检验c=-符合题意.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    设函数f(x)满足2f(x)-f()=4x-+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
    (1)求f(x)的解析式.
    (2)求{bn}的通项公式bn.
    (3)试比较2an与bn的大小,并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    等差数列{an}中,a7=4,a19=2a9.
    (1)求{an}的通项公式;
    (2)设bn=,求数列{bn}的前n项和Sn.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    如图，互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上，所有AnBn相互平行，且所有梯形AnBnBn＋1An＋1的面积均相等，设OAn＝an.若a1＝1，a2＝2，则数列{an}的通项公式是________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

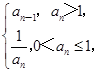    若数列{an}满足：存在正整数T，对于任意正整数n都有an＋T＝an成立，则称数列{an}为周期数列，周期为T.已知数列{an}满足a1＝m(m＞0)，an＋1＝则下列结论中错误的是(　　)
    A．若m＝，则a5＝3
    B．若a3＝2，则m可以取3个不同的值
    C．若m＝，则数列{an}是周期为3的数列
    D．?m∈Q且m≥2，使得数列{an}是周期数列

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知数列{an}为等差数列,公差为d,若<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为(　　)
    A．11B．19C．20D．21

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

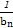    已知各项都不相等的等差数列{an}的前6项和为60,且a6为a1和a21的等比中项.
    (1)求数列{an}的通项公式.
    (2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=3,求数列{}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    数列{an}是公差不为0的等差数列,且a1,a3,a7为等比数列{bn}的连续三项,则数列{bn}的公比为(　　)
    A．B．4C．2D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知数列{an}满足anan＋1an＋2·an＋3＝24，且a1＝1，a2＝2，a3＝3，则a1＋a2＋a3＋…＋a2 013＝________.

    查看答案和解析>>

    同步练习册答案