【题目】如图，三棱柱
中，
，
，
.
（1）证明：
；
（2）若平面
平面
，
，求二面角
的余弦值.
【答案】（1）详见解析（2）
【解析】
（1）取AB的中点O，连接OC，OA1，A1B，由已知可证OA1⊥AB，AB⊥平面OA1C，进而可得AB⊥A1C；
（2）易证OA，OA1，OC两两垂直．以O为坐标原点，
的方向为x轴的正向，||为单位长，建立坐标系，求出平面
平面BB1C1C的法向量，代入向量夹角公式，可得答案．
（1）取
中点
，连接
，
，因为
，所以
；
因为
，
，故
为等边三角形，所以
；
因为
，所以
平面
；所以
.
（2）由（1）可知，，，又因为平面
平面
，交线为，所以
平面，故
，，两两垂直.以为坐标原点，建立空间直角坐标系
如图，
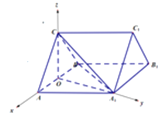
因为
，所以
，所以
，
，
，
.
设
是平面
的法向量，则
，
，解得
，同理可得，平面
的法向量
，
，
，
所以二面角余弦值为.
每日10分钟口算心算速算天天练系列答案科目：高中数学 来源： 题型：
【题目】随着网络的发展，网上购物越来越受到人们的喜爱，各大购物网站为增加收入，促销策略越来越多样化，促销费用也不断增加.下表是某购物网站2017年1-8月促销费用（万元）和产品销量（万件）的具体数据.
（1）根据数据绘制的散点图能够看出可用线性回归模型拟合
与
的关系，请用相关系数
加以说明；（系数精确到0.001）
（2）建立
关于
的回归方程
（系数精确到0.01）；如果该公司计划在9月份实现产品销量超6万件，预测至少需投入促销费用多少万元（结果精确到0.01）.
参考数据： 
， 
， 
， 
， 
，其中
， 
分别为第
个月的促销费用和产品销量， 
.
参考公式：（1）样本
的相关系数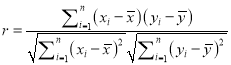
（2）对于一组数据
， 
， 
， 
，其回归方程
的斜率和截距的最小二乘估计分别为
， 
.
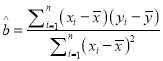查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f(x)是R上的奇函数，且当x>0时，f(x)＝－x2＋2x＋2.
(1)求f(x)的解析式；
(2)画出f(x)的图像，并指出f(x)的单调区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,一张矩形白纸ABCD,AB=10,AD=
,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)
①当平面ABE∥平面CDF时,AC∥平面BFDE
②当平面ABE∥平面CDF时,AE∥CD
③当A、C重合于点P时,PG⊥PD
④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司计划在办公大厅建一面长为
米的玻璃幕墙.先等距安装
根立柱，然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元，一块长为
米的玻璃造价为
元.假设所有立柱的粗细都忽略不计，且不考虑其他因素，记总造价为
元（总造价=立柱造价+玻璃造价）.
（1）求关于的函数关系式；
（2）当
时，怎样设计能使总造价最低？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
的参数方程为
（
为参数，
），以
为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
．
（Ⅰ）求直线的普通方程和曲线的直角坐标方程；
（Ⅱ）设
，直线交曲线于
两点，
是直线上的点，且
，当
最大时，求点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等比数列{an}的各项均为正数，且a1＋2a2＝5，4a＝a2a6.
(1)求数列{an}的通项公式；
(2)若数列{bn}满足b1＝2，且bn＋1＝bn＋an，求数列{bn}的通项公式；
(3)设
，求数列{cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
