
【题目】当![]() 时,若函数
时,若函数![]() 的图象与
的图象与![]() 的图象有且只有一个交点,则正实数
的图象有且只有一个交点,则正实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据题意,由二次函数的性质分析可得![]() 为二次函数,在区间
为二次函数,在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数,分
为增函数,分![]() 和
和![]() 两种情况,结合图象分析两个函数的单调性与值域,即可得出正实数
两种情况,结合图象分析两个函数的单调性与值域,即可得出正实数![]() 的取值范围.
的取值范围.
解:当![]() 时,又因为
时,又因为![]() 为正实数,
为正实数,
函数![]() 的图象二次函数,
的图象二次函数,
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数;
为增函数;
函数![]() ,是斜率为
,是斜率为![]() 的一次函数.
的一次函数.
最小值为![]() ,最大值为
,最大值为![]() ;
;
①当![]() 时,即
时,即![]() 时,
时,
函数![]() 在区间
在区间![]() 为减函数,
为减函数,
![]() 在区间
在区间![]() 为增函数,
为增函数,
![]() 的图象与
的图象与![]() 的图象有且只有一个交点,
的图象有且只有一个交点,
则![]() ,
,![]() 即
即
![]() ,解得
,解得![]() ,
,
所以![]()
②当![]() 时,即
时,即![]() 时,
时,
函数![]() 在区间
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数,
为增函数,
![]() 在区间
在区间![]() 为增函数,
为增函数,
![]() 的图象与
的图象与![]() 的图象有且只有一个交点,
的图象有且只有一个交点,
则![]() ,
,![]() 即
即
![]() 的图象与
的图象与![]() 的图象有且只有一个交点
的图象有且只有一个交点
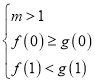 ,
,
解得![]() 或
或![]()
综上所述:正实数![]() 的取值范围为
的取值范围为![]() .
.
故选:B


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若在这50名被调查者中随机发出20份的调查问卷,记![]() 为所发到的20人中赞成“车辆限行”的人数,求使概率
为所发到的20人中赞成“车辆限行”的人数,求使概率![]() 取得最大值的整数
取得最大值的整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为3的线段![]() 的两端点
的两端点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上移动,
轴上移动,![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)过![]() 作互相垂直的两条直线分别与轨迹
作互相垂直的两条直线分别与轨迹![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() ,设
,设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,试探究直线
,试探究直线![]() 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+2φ)为偶函数,其中φ∈(0,![]() ),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
A.g(x)在区间[![]() ]上的最小值为﹣1
]上的最小值为﹣1
B.g(x)的图象可由函数f(x)的图象向上平移一个单位,再向右平移![]() 个单位长度得到
个单位长度得到
C.g(x)的图象的一个对称中心为(![]() ,0)
,0)
D.g(x)的一个单调递增区间为[0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 、
、![]() 的中点,对于平面
的中点,对于平面![]() 截四棱锥
截四棱锥![]() 所得的截面多边形,有以下三个结论:
所得的截面多边形,有以下三个结论:
①截面的面积等于![]() ;
;
②截面是一个五边形;
③截面只与四棱锥![]() 四条侧棱中的三条相交.
四条侧棱中的三条相交.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() 且不过点
且不过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(Ⅰ)若![]() 垂直于
垂直于![]() 轴,求直线
轴,求直线![]() 的斜率;
的斜率;
(Ⅱ)试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠病毒是一种通过飞沫和接触传播的变异病毒,为筛查该病毒,有一种检验方式是检验血液样本相关指标是否为阳性,对于![]() 份血液样本,有以下两种检验方式:一是逐份检验,则需检验
份血液样本,有以下两种检验方式:一是逐份检验,则需检验![]() 次.二是混合检验,将其中
次.二是混合检验,将其中![]() 份血液样本分别取样混合在一起,若检验结果为阴性,那么这
份血液样本分别取样混合在一起,若检验结果为阴性,那么这![]() 份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这![]() 份血液究竟哪些为阳性,就需要对它们再逐份检验,此时
份血液究竟哪些为阳性,就需要对它们再逐份检验,此时![]() 份血液检验的次数总共为
份血液检验的次数总共为![]() 次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为
次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为![]() .
.
(Ⅰ)求把2份血液样本混合检验结果为阳性的概率;
(Ⅱ)若检验次数的期望值越小,则方案越“优”.方案一、二、三中哪个最“优”?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com