
【题目】已知函数![]() (
(![]() 自然对数的底数)有两个零点.
自然对数的底数)有两个零点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() 的两个零点分别为
的两个零点分别为![]()
![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)将![]() 有两个零点问题,转化为
有两个零点问题,转化为![]() 有两个零点,利用
有两个零点,利用![]() 研究
研究![]() 的单调性和零点,由此求得
的单调性和零点,由此求得![]() 的取值范围.
的取值范围.
(2)将所要证明的不等式转化为证明![]() ,构造函数
,构造函数![]() ,利用
,利用![]() 证得
证得![]() ,由此证得不等式成立.
,由此证得不等式成立.
(1)![]() 有两个零点,等价于
有两个零点,等价于![]() 有两个零点,令
有两个零点,令![]() ,则
,则![]() 在
在![]() 时恒成立,所以
时恒成立,所以![]() 在
在![]() 时单调递增,
时单调递增,
所以![]() 有两个零点,等价于
有两个零点,等价于![]() 有两个零点.
有两个零点.
因为![]() 所以
所以
①当![]() 时,
时,![]() ,
,![]() 单调递增,不可能有两个零点;
单调递增,不可能有两个零点;
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,![]() 单调递增;令
单调递增;令![]() ,得
,得![]() ,
,![]() 单调递减.
单调递减.
所以![]() .
.
若![]() ,得
,得![]() ,此时
,此时![]() 恒成立,没有零点;
恒成立,没有零点;
若![]() ,得
,得![]() ,此时
,此时![]() 有一个零点;
有一个零点;
若![]() ,得
,得![]() ,因为
,因为![]() ,且
,且![]() ,
,![]() ,所以
,所以![]() 在
在![]() ,
,![]() 上各存在一个零点,符合题意.
上各存在一个零点,符合题意.
综上,当![]() 时,函数
时,函数![]() 有两个零点,
有两个零点,
即若函数![]() 有两个零点,则
有两个零点,则![]() 的取值范围为
的取值范围为![]() .
.
(2)要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,
,
由(1)知![]() ,
,![]() ,所以只需证
,所以只需证![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以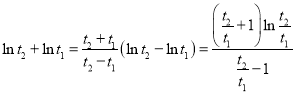 ,只需证
,只需证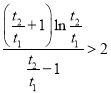 .
.
设![]() ,令
,令![]() ,则
,则![]() ,所以只需证
,所以只需证![]() ,即证
,即证![]() .
.
令![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
即当![]() 时,
时,![]() 成立.
成立.
所以![]() ,即
,即![]() ,
,
即![]() .
.


科目:高中数学 来源: 题型:
【题目】在极坐标系中,方程C:![]() 表示的曲线被称作“四叶玫瑰线”(如图)
表示的曲线被称作“四叶玫瑰线”(如图)

(1)求以极点为圆心的单位圆与四叶玫瑰线交点的极坐标和直角坐标;
(2)直角坐标系的原点与极点重合,x轴正半轴与极轴重合.求直线l:![]() 上的点M与四叶攻瑰线上的点N的距离的最小值.
上的点M与四叶攻瑰线上的点N的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5B.21元C.21.5元D.22元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为彻底打赢脱贫攻坚战,2020年春,某市政府投入资金帮扶某农户种植蔬菜大棚脱贫致富,若该农户计划种植冬瓜和茄子,总面积不超过15亩,帮扶资金不超过4万元,冬瓜每亩产量10 000斤,成本2000元,每斤售价0.5元,茄子每亩产量5000斤,成本3000元,每斤售价1.4元,则该农户种植冬瓜和茄子利润的最大值为( )
A.4万元B.5.5万元C.6.5万元D.10万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)
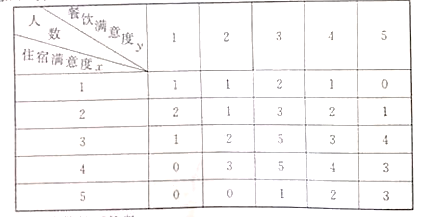
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一场突如其来的新冠肺炎疫情在全国蔓延,在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,共抗疫情。每天测量体温也就成为了所有人的一项责任,一般认为成年人腋下温度![]() (单位:℃)平均在36℃~37℃之间即为正常体温,超过37.1℃即为发热。发热状态下,不同体温可分成以下三种发热类型:低热:
(单位:℃)平均在36℃~37℃之间即为正常体温,超过37.1℃即为发热。发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .
.
某位患者因发热,虽排除肺炎,但也于12日至26日住院治疗. 医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热. 住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用“抗生素A”治疗 | 使用“抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温(℃) | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用“抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温(℃) | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(1)请你计算住院期间该患者体温不低于39℃的各天体温平均值;
(2)在18日—22日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“![]() 项目”的检查,求至少两天在高热体温下做“
项目”的检查,求至少两天在高热体温下做“![]() 项目”检查的概率;
项目”检查的概率;
(3)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四面体P-ABC的棱长均为a,O为正四面体P-ABC的外接球的球心,过点O作平行于底面ABC的平面截正四面体P-ABC,得到三棱锥P-A1B1C1和三棱台ABC-A1B1C1,那么三棱锥P-A1B1C1的外接球的表面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com