
【题目】已知函数![]() .
.
(1)若函数![]() 的图象与
的图象与![]() 轴无交点,求
轴无交点,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 上存在零点,求
上存在零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得方程f(x)=0的根的判别式△<0,解不等式即可得到范围;
(2)求出二次函数的对称轴方程,判断f(x)在[﹣1,1]的单调性,再由零点的定义可得f(1)≤0,f(﹣1)≥0,解不等式即可得到所求范围.
(1)若函数y=f(x)的图象与x轴无交点,
则方程f(x)=0的根的判别式Δ<0,即16-4(a+3)<0,
解得a>1.
故a的取值范围为a>1.
(2)因为函数f(x)=x2-4x+a+3图象的对称轴是x=2,
所以y=f(x)在[-1,1]上是减函数.
又y=f(x)在[-1,1]上存在零点,
所以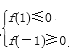 ,即
,即![]() ,
,
解得-8≤a≤0.
故实数a的取值范围为-8≤a≤0.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交
交![]() 于B,C两点.
于B,C两点.
(1)若![]() 垂直于轴,且线段BC的长为1,求
垂直于轴,且线段BC的长为1,求![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,求
,求![]() ;
;
(3)设抛物线上异于![]() 的点A满足
的点A满足![]() ,若
,若![]() 的重心在
的重心在![]() 轴上,求
轴上,求![]() 的重心的坐标.
的重心的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列性质的函数![]() 的全体;在定义域内存在实数t,使得
的全体;在定义域内存在实数t,使得![]() .
.
(1)判断![]() 是否属于集合M,并说明理由;
是否属于集合M,并说明理由;
(2)若![]() 属于集合M,求实数a的取值范围;
属于集合M,求实数a的取值范围;
(3)若![]() ,求证:对任意实数b,都有
,求证:对任意实数b,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次数学考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班样本成绩的茎叶图如图所示.
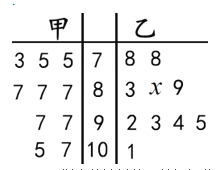
(1)用样本估计总体,若根据茎叶图计算得甲乙两个班级的平均分相同,求![]() 的值;
的值;
(2)从甲班的样本不低于90分的成绩中任取2名学生的成绩,求这2名学生的成绩不相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com