
【题目】2016年1月1日,我国实行全面二孩政策,同时也对妇幼保健工作提出了更高的要求.某城市实行网格化管理,该市妇联在网格1与网格2两个区域内随机抽取12个刚满8个月的婴儿的体重信息,体重分布数据的茎叶图如图所示(单位:斤,2斤![]() 1千克),体重不超过
1千克),体重不超过![]() 千克的为合格.
千克的为合格.

(1)从网格1与网格2分别随机抽取2个婴儿,求网格1至少有一个婴儿体重合格且网格2至少有一个婴儿体重合格的概率;
(2)妇联从网格1内8个婴儿中随机抽取4个进行抽检,若至少2个婴儿合格,则抽检通过,若至少3个合格,则抽检为良好,求网格1在抽检通过的条件下,获得抽检为良好的概率;
(3)若从网格1与网格2内12个婴儿中随机抽取2个,用![]() 表示网格2内婴儿的个数,求
表示网格2内婴儿的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】试题分析: (1)根据茎叶图得出网格1内体重合格的婴儿数和网格2内体重合格的婴儿数,运用对立事件的概率求解即可;(2)分别求出网格1在抽检通过的概率和获得抽检为良好的概率,运用条件概率求解即可;(3) 由题意得出所有x的可能取值,分别求出概率列成表格形式得出分布列,根据定义求得期望值.
试题解析:
(1)由茎叶图知,网格1内体重合格的婴儿数为4,网格2内体重合格的婴儿数为2,则所求概率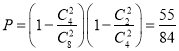 .
.
(2)设事件![]() 表示“2个合格,2个不合格”;事件
表示“2个合格,2个不合格”;事件![]() 表示“3个合格,1个不合格”; 事件
表示“3个合格,1个不合格”; 事件![]() 表示“4个全合格”;事件
表示“4个全合格”;事件![]() 表示“抽检通过”;事件
表示“抽检通过”;事件![]() 表示“抽检良好”.
表示“抽检良好”.
∴![]() ,
,
![]() ,则所求概率
,则所求概率![]() .
.
(3)由题意知, ![]() 的所有可能取值为0,1,2.
的所有可能取值为0,1,2.
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 的分布列为
的分布列为
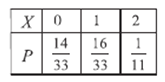
∴![]() .
.
点睛:在求某事件的概率时,若事件较为复杂,可通过求它的对立事件的概率来求解,对于含有”至多”,”至少”等词语的概率问题时,一般用对立事件的概率来解较为简单;求概率时,当题目中含有”在…发生的条件下,求…发生的概率”时,一般用条件概率求解,解题时分清楚谁是条件,然后利用公式求解.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() 使得关于
使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y与x的函数图象,给出下列四种说法,①图(2)对应的方案是:提高票价,并提高成本;②图(2)对应的方案是:保持票价不变,并降低成本;③图(3)对应的方案是:提高票价,并保持成本不变;④图(3)对应的方案是:提高票价,并降低成本.其中,正确的说法是( )

A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
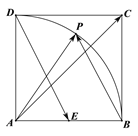
【题目】如图,在边长为1的正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧(在正方形内,包括边界点)上的任意一点,则![]() 的取值范围是________; 若向量
的取值范围是________; 若向量![]() ,则
,则![]() 的最小值为_________.
的最小值为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 为焦点是
为焦点是![]() 的抛物线上一点,
的抛物线上一点, ![]() 为直线
为直线![]() 上任一点,
上任一点, ![]() 分别为椭圆
分别为椭圆![]() 的上,下顶点,且
的上,下顶点,且![]() 三点的连线可以构成三角形.
三点的连线可以构成三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点分别交于点
的另一交点分别交于点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品每千克定价10元,商家采取了如下的促销方式:
一次购买量 | 促销方式 |
不多于20千克 | 原价出售 |
多于20千克且不多于40千克 | 不多于20千克部分,原价出售 多于20千克部分,九折出售 |
多于40千克 | 不多于20千克部分,原价出售 多于20千克且不多于40千克部分,九折出售 多于40千克部分八折出售 |
(1)求一次购买![]() (单位:千克),此商品的花费
(单位:千克),此商品的花费![]() (单位:元)的函数解析式;
(单位:元)的函数解析式;
(2)某人一次购买此商品400元,问他能购得此商品多少千克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.各个面都是三角形的几何体是三棱锥
B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥
C.棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com