
【题目】执行如图所示的程序框图,设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出的S的值为n,则m+n=
科目:高中数学 来源: 题型:
【题目】已知某公司生产一种品牌服装的年固定成本为10万元,且每生产1万件,需要另投入1.9万元.设R(x)(单位:万元)为销售收入,根据市场调查知R(x)= 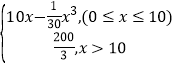 其中x(单位:万件)是年产量.
其中x(单位:万件)是年产量.
(1)写出年利润W(单位:万元)关于年产量x的函数解析式.
(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句中是命题的有________,其中是真命题的有_____(填序号).
①“垂直于同一条直线的两个平面必平行吗?”②“一个数不是正数就是负数”;③“在一个三角形中,大角所对的边大于小角所对的边”;④“若x+y为有理数,则x,y都是有理数”;⑤作一个三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量,若一天中从甲地去乙地的旅客人数不超过900的概率为p0,则p0的值为 ( )
A. 0.954 4 B. 0.682 6 C. 0.997 4 D. 0.977 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图所示的频率分布直方图.

(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表).
和样本方差s2(同一组中的数据用该组区间的中点值作代表).
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
①利用该正态分布,求P(187.8<Z<212.2);
②某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)上的产品件数,利用①的结果,求E(X).
附:![]() ≈12.2.
≈12.2.
若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3-3(a+1)x2+6ax+8,其中a∈R.
(1)若f(x)在x=3处取得极值,求常数a的值;
(2)若f(x)在(-∞,0)上为增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣2x,其中a≤0.
ax2﹣2x,其中a≤0.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+b,求a﹣2b的值;
(2)讨论函数f(x)的单调性;
(3)设函数g(x)=x2﹣3x+3,如果对于任意的x,t∈(0,1],都有f(x)≤g(t)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C所对边的边长,且C=![]() ,a+b=λc(其中λ>1).
,a+b=λc(其中λ>1).
(1)若λ=![]() 时,证明:△ABC为直角三角形;
时,证明:△ABC为直角三角形;
(2)若![]() ·
·![]() =
=![]() λ2,且c=3,求λ的值.
λ2,且c=3,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,已知a1≠0,2an﹣a1=S1Sn , n∈N* .
(1)求a1a2 , 并求数列{an}的通项公式,
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com