
【题目】已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+![]() t≤t2,求实数t的取值范围.
t≤t2,求实数t的取值范围.
科目:高中数学 来源: 题型:
【题目】在改革开放40年成就展上某地区某农产品近几年的产量统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)根据线性回归方程预测2020年该地区该农产品的年产量.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为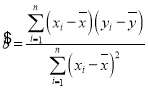 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留到小数点后两位)
,计算结果保留到小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“互倒函数”的定义如下:对于定义域内每一个![]() ,都有
,都有![]() 成立,若现在已知函数
成立,若现在已知函数![]() 是定义域在
是定义域在![]() 的“互倒函数”,且当
的“互倒函数”,且当![]() 时,
时,![]() 成立.若函数
成立.若函数![]() (
(![]() )都恰有两个不同的零点,则实数
)都恰有两个不同的零点,则实数![]() 的取值范围是( )
的取值范围是( )
A.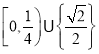 B.
B.![]() C.
C.![]() D.
D.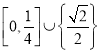
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,整理如下:
甲公司员工![]() :410,390,330,360,320,400,330,340,370,350
:410,390,330,360,320,400,330,340,370,350
乙公司员工![]() :360,420,370,360,420,340,440,370,360,420
:360,420,370,360,420,340,440,370,360,420
每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件0.65元,乙公司规定每天350件以内(含350件)的部分每件0.6元,超出350件的部分每件0.9元.
(1)根据题中数据写出甲公司员工![]() 在这10天投递的快件个数的平均数和众数;
在这10天投递的快件个数的平均数和众数;
(2)为了解乙公司员工![]() 每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为
每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据题中数据估算两公司被抽取员工在该月所得的劳务费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com