分析:(1)分别把n=5,4,3,2代入a
n+1=a
n2-2na
n+2,分别求出a
1=3,a
2=5,a
3=7,a
4=9,从而猜想:a
n=2n+1.
(2)
cn===(-)Tn=c1+c2++cn=[(1-)+(-)++(-)]=
(1-)而对于任意n∈N
*Tn+1-Tn=(1-)-(1-)=
>0.数列T
n是递增数列,T
n的最小值为T
1=,由此可求出存在最大的整数7,使得对任意正整数n,均有T
n>
成立.
解答:解:(1)由a
5=11,得11=a
42-8a
4+2,解得a
4=9或a
4=-1(舍去)
由a
4=9,得9=a
32-6a
3+2,解得a
3=7或a
3=-1(舍去)
由a
3=7,得7=a
22-4a
2+2,解得a
2=5或a
2=-1(舍去)
由a
2=5,得5=a
12-2a
1+2,解得a
1=3或a
1=-1(舍去)∴a
1=3,a
2=5,a
3=7,a
4=9
猜想:a
n=2n+1
(2)
cn==
=
(-)T
n=c
1+c
2++c
n=
[(1-)+(-)++(-)]=
(1-)而对于任意n∈N
*Tn+1-Tn=(1-)-(1-)=
>0∴数列T
n是递增数列
∴T
n的最小值为T
1=要使T
n>
对任意n∈N
•总成立,只要T
1>
即
<
,∴m<8
又m∈N
•,因此存在最大的整数7,使得对任意正整数n,均有T
n>
成立
点评:本题考查数列和不等式的综合应用题,解题时要注意公式的灵活运用,合理地进行等价转化.



 ,是否存在最大的整数m,使得对任意正整数n,均有
,是否存在最大的整数m,使得对任意正整数n,均有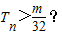 若存在,求出m的值;若不存在,请说明理由.
若存在,求出m的值;若不存在,请说明理由.