
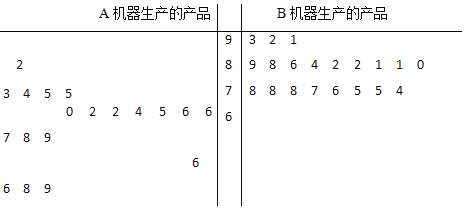
ΓΨΧβΡΩΓΩΡ≥ΙΛ≥ß”–ΝΫΧ®≤ΜΆ§ΜζΤςAΚΆB…ζ≤ζΆ§“Μ÷÷≤ζΤΖΗς10ΆρΦΰΘ§œ÷¥”ΗςΉ‘…ζ≤ζΒΡ≤ζΤΖ÷–Ζ÷±πΥφΜζ≥ι»Γ20ΦΰΘ§Ϋχ––ΤΖ÷ ΦχΕ®Θ§ΦχΕ®≥…Φ®ΒΡΨΞ“ΕΆΦ»γΆΦΥυ ΨΘΚ
ΗΟ≤ζΤΖΒΡ÷ ΝΩΤάΦέ±ξΉΦΙφΕ®ΘΚΦχΕ®≥…Φ®¥οΒΫ![]() ΒΡ≤ζΤΖΘ§÷ ΝΩΒ»ΦΕΈΣ”≈–ψΘΜΦχΕ®≥…Φ®¥οΒΫ
ΒΡ≤ζΤΖΘ§÷ ΝΩΒ»ΦΕΈΣ”≈–ψΘΜΦχΕ®≥…Φ®¥οΒΫ![]() ΒΡ≤ζΤΖΘ§÷ ΝΩΒ»ΦΕΈΣΝΦΚΟΘΜΦχΕ®≥…Φ®¥οΒΫ
ΒΡ≤ζΤΖΘ§÷ ΝΩΒ»ΦΕΈΣΝΦΚΟΘΜΦχΕ®≥…Φ®¥οΒΫ![]() ΒΡ≤ζΤΖΘ§÷ ΝΩΒ»ΦΕΈΣΚœΗώ
ΒΡ≤ζΤΖΘ§÷ ΝΩΒ»ΦΕΈΣΚœΗώ![]() ΫΪ’βΉι ΐΨίΒΡΤΒ¬ ”ΈΣ’ϊ≈ζ≤ζΤΖΒΡΗ≈¬ Θ°
ΫΪ’βΉι ΐΨίΒΡΤΒ¬ ”ΈΣ’ϊ≈ζ≤ζΤΖΒΡΗ≈¬ Θ°
![]() Δώ
Δώ![]() ¥”Β»ΦΕΈΣ”≈–ψΒΡ―υ±Ψ÷–ΥφΜζ≥ι»ΓΝΫΦΰΘ§Φ«XΈΣά¥Ή‘BΜζΤς…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΘ§–¥≥ωXΒΡΖ÷≤ΦΝ–Θ§≤Δ«σXΒΡ ΐ―ßΤΎΆϊΘΜ
¥”Β»ΦΕΈΣ”≈–ψΒΡ―υ±Ψ÷–ΥφΜζ≥ι»ΓΝΫΦΰΘ§Φ«XΈΣά¥Ή‘BΜζΤς…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΘ§–¥≥ωXΒΡΖ÷≤ΦΝ–Θ§≤Δ«σXΒΡ ΐ―ßΤΎΆϊΘΜ
![]() Δρ
Δρ![]() Άξ≥…œ¬Ν–
Άξ≥…œ¬Ν–![]() Ν–ΝΣ±μΘ§“‘≤ζΤΖΒ»ΦΕ «Ζώ¥οΒΫΝΦΚΟ“‘…œ
Ν–ΝΣ±μΘ§“‘≤ζΤΖΒ»ΦΕ «Ζώ¥οΒΫΝΦΚΟ“‘…œ![]() Κ§ΝΦΚΟ
Κ§ΝΦΚΟ![]() ΈΣ≈–Εœ“άΨίΘ§≈–ΕœΡή≤ΜΡή‘ΎΈσ≤ν≤Μ≥§Ιΐ
ΈΣ≈–Εœ“άΨίΘ§≈–ΕœΡή≤ΜΡή‘ΎΈσ≤ν≤Μ≥§Ιΐ![]() ΒΡ«ιΩωœ¬Θ§»œΈΣBΜζΤς…ζ≤ζΒΡ≤ζΤΖ±»AΜζΤς…ζ≤ζΒΡ≤ζΤΖΚΟΘΜ
ΒΡ«ιΩωœ¬Θ§»œΈΣBΜζΤς…ζ≤ζΒΡ≤ζΤΖ±»AΜζΤς…ζ≤ζΒΡ≤ζΤΖΚΟΘΜ
A…ζ≤ζΒΡ≤ζΤΖ | B…ζ≤ζΒΡ≤ζΤΖ | ΚœΦΤ | |
ΝΦΚΟ“‘…œ | |||
ΚœΗώ | |||
ΚœΦΤ |
![]() “―÷Σ”≈–ψΒ»ΦΕ≤ζΤΖΒΡάϊ»σΈΣ12‘Σ
“―÷Σ”≈–ψΒ»ΦΕ≤ζΤΖΒΡάϊ»σΈΣ12‘Σ![]() ΦΰΘ§ΝΦΚΟΒ»ΦΕ≤ζΤΖΒΡάϊ»σΈΣ10‘Σ
ΦΰΘ§ΝΦΚΟΒ»ΦΕ≤ζΤΖΒΡάϊ»σΈΣ10‘Σ![]() ΦΰΘ§ΚœΗώΒ»ΦΕ≤ζΤΖΒΡάϊ»σΈΣ5‘Σ
ΦΰΘ§ΚœΗώΒ»ΦΕ≤ζΤΖΒΡάϊ»σΈΣ5‘Σ![]() ΦΰΘ§AΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡ≥…±ΨΈΣ20Άρ‘ΣΘ§BΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡ≥…±ΨΈΣ30Άρ‘ΣΘΜΗΟΙΛ≥ßΨωΕ®ΘΚΑ¥―υ±Ψ ΐΨί≤βΥψΘ§ΝΫ÷÷ΜζΤςΖ÷±π…ζ≤ζ10ΆρΦΰ≤ζΤΖΘ§»τ ’“φ÷°≤ν¥οΒΫ5Άρ‘Σ“‘…œΘ§‘ρΧ‘Χ≠ ’“φΒΆΒΡΜζΤςΘ§»τ ’“φ÷°≤ν≤Μ≥§Ιΐ5Άρ‘ΣΘ§‘ρ»‘»Μ±ΘΝτ‘≠ά¥ΒΡΝΫΧ®ΜζΤς
ΦΰΘ§AΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡ≥…±ΨΈΣ20Άρ‘ΣΘ§BΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡ≥…±ΨΈΣ30Άρ‘ΣΘΜΗΟΙΛ≥ßΨωΕ®ΘΚΑ¥―υ±Ψ ΐΨί≤βΥψΘ§ΝΫ÷÷ΜζΤςΖ÷±π…ζ≤ζ10ΆρΦΰ≤ζΤΖΘ§»τ ’“φ÷°≤ν¥οΒΫ5Άρ‘Σ“‘…œΘ§‘ρΧ‘Χ≠ ’“φΒΆΒΡΜζΤςΘ§»τ ’“φ÷°≤ν≤Μ≥§Ιΐ5Άρ‘ΣΘ§‘ρ»‘»Μ±ΘΝτ‘≠ά¥ΒΡΝΫΧ®ΜζΤς![]() Ρψ»œΈΣΗΟΙΛ≥ßΜα»‘»Μ±ΘΝτ‘≠ά¥ΒΡΝΫΧ®ΜζΤς¬πΘΩ
Ρψ»œΈΣΗΟΙΛ≥ßΜα»‘»Μ±ΘΝτ‘≠ά¥ΒΡΝΫΧ®ΜζΤς¬πΘΩ
ΗΫΘΚ![]() ΕάΝΔ–‘Φλ―ιΦΤΥψΙΪ ΫΘΚ
ΕάΝΔ–‘Φλ―ιΦΤΥψΙΪ ΫΘΚ![]() Θ°
Θ°
![]() ΝΌΫγ÷Β±μΘΚ
ΝΌΫγ÷Β±μΘΚ
|
|
|
|
|
|
k |
|
|
|
|
|
ΓΨ¥πΑΗΓΩΘ®IΘ©œξΦϊΫβΈωΘΜΘ®IIΘ©œξΦϊΫβΈωΘΜΘ®IIIΘ©≤ΜΜα.
ΓΨΫβΈωΓΩ
![]() Δώ
Δώ![]() ¥”Β»ΦΕΈΣ”≈–ψΒΡ―υ±Ψ÷–ΥφΜζ≥ι»ΓΝΫΦΰΘ§Φ«XΈΣά¥Ή‘BΜζΤς…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΘ§«σ≥ωXΒΡΩ…Ρή÷ΒΘ§«σ≥ωΗωΘΜ«σ≥ωΗ≈¬ –¥≥ωXΒΡΖ÷≤ΦΝ–Θ§≤Δ»ΜΚσ«σXΒΡ ΐ―ßΤΎΆϊΘΜ
¥”Β»ΦΕΈΣ”≈–ψΒΡ―υ±Ψ÷–ΥφΜζ≥ι»ΓΝΫΦΰΘ§Φ«XΈΣά¥Ή‘BΜζΤς…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΘ§«σ≥ωXΒΡΩ…Ρή÷ΒΘ§«σ≥ωΗωΘΜ«σ≥ωΗ≈¬ –¥≥ωXΒΡΖ÷≤ΦΝ–Θ§≤Δ»ΜΚσ«σXΒΡ ΐ―ßΤΎΆϊΘΜ
![]() Δρ
Δρ![]() Άξ≥…œ¬Ν–
Άξ≥…œ¬Ν–![]() Ν–ΝΣ±μΘ§«σ≥ω
Ν–ΝΣ±μΘ§«σ≥ω![]() Θ§»ΜΚσ≈–Εœ“‘≤ζΤΖΒ»ΦΕ «Ζώ¥οΒΫΝΦΚΟ“‘…œ
Θ§»ΜΚσ≈–Εœ“‘≤ζΤΖΒ»ΦΕ «Ζώ¥οΒΫΝΦΚΟ“‘…œ![]() Κ§ΝΦΚΟ
Κ§ΝΦΚΟ![]() ΈΣ≈–Εœ“άΨίΘ§≈–ΕœΡή≤ΜΡή‘ΎΈσ≤ν≤Μ≥§Ιΐ
ΈΣ≈–Εœ“άΨίΘ§≈–ΕœΡή≤ΜΡή‘ΎΈσ≤ν≤Μ≥§Ιΐ![]() ΒΡ«ιΩωœ¬Θ§»œΈΣBΜζΤς…ζ≤ζΒΡ≤ζΤΖ±»AΜζΤς…ζ≤ζΒΡ≤ζΤΖΚΟΘΜ
ΒΡ«ιΩωœ¬Θ§»œΈΣBΜζΤς…ζ≤ζΒΡ≤ζΤΖ±»AΜζΤς…ζ≤ζΒΡ≤ζΤΖΚΟΘΜ
![]() «σ≥ωΝΫ÷÷ΜζΤςΒΡάϊ»σΘ§»ΜΚσ±»ΫœΦ¥Ω…Θ°
«σ≥ωΝΫ÷÷ΜζΤςΒΡάϊ»σΘ§»ΜΚσ±»ΫœΦ¥Ω…Θ°
![]() Δώ
Δώ![]() ¥”ΨΞ“ΕΆΦΩ…“‘÷ΣΒάΘ§―υ±Ψ÷–”≈–ψΒΡ≤ζΤΖ”–2Ηωά¥Ή‘AΜζΤςΘ§3Ηωά¥Ή‘BΜζΤςΘΜ
¥”ΨΞ“ΕΆΦΩ…“‘÷ΣΒάΘ§―υ±Ψ÷–”≈–ψΒΡ≤ζΤΖ”–2Ηωά¥Ή‘AΜζΤςΘ§3Ηωά¥Ή‘BΜζΤςΘΜ
Υυ“‘XΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§![]()
![]() Θ§
Θ§![]() Θ§
Θ§![]()
XΒΡΖ÷≤ΦΝ–ΈΣΘΚ
X | 0 | 1 | 2 |
P |
|
|
|
Υυ“‘
![]() Δρ
Δρ![]() ”…“―÷ΣΩ…ΒΟΘ§
”…“―÷ΣΩ…ΒΟΘ§![]() Ν–ΝΣ±μΈΣ
Ν–ΝΣ±μΈΣ
A…ζ≤ζΒΡ≤ζΤΖ | B…ζ≤ζΒΡ≤ζΤΖ | ΚœΦΤ | |
ΝΦΚΟ“‘…œ | 6 | 12 | 18 |
ΚœΗώ | 14 | 8 | 22 |
ΚœΦΤ | 20 | 20 | 40 |
![]() Θ§
Θ§
Υυ“‘≤ΜΡή‘ΎΈσ≤ν≤Μ≥§Ιΐ![]() ΒΡ«ιΩωœ¬Θ§»œΈΣ≤ζΤΖΒ»ΦΕ «Ζώ¥οΒΫΝΦΚΟ“‘…œ”κ…ζ≤ζ≤ζΤΖΒΡΜζΤς”–ΙΊ
ΒΡ«ιΩωœ¬Θ§»œΈΣ≤ζΤΖΒ»ΦΕ «Ζώ¥οΒΫΝΦΚΟ“‘…œ”κ…ζ≤ζ≤ζΤΖΒΡΜζΤς”–ΙΊ![]()
![]() ΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡάϊ»σΈΣ
ΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡάϊ»σΈΣ![]() Άρ‘ΣΘ§
Άρ‘ΣΘ§
BΜζΤςΟΩ…ζ≤ζ10ΆρΦΰΒΡάϊ»σΈΣ![]() Άρ‘ΣΘ§
Άρ‘ΣΘ§
Υυ“‘![]() Θ§
Θ§
Υυ“‘ΗΟΙΛ≥ß≤ΜΜα»‘»Μ±ΘΝτ‘≠ά¥ΒΡΝΫΧ®ΜζΤςΘ§”ΠΗΟΜα¬τΒτAΜζΤςΘ§Ά§ ±ΙΚ¬ρ“ΜΧ®BΜζΤς![]()



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“–ΘΒΡΩΈΆβΉέΚœ ΒΦυ―–ΨΩ–ΓΉι”ϊ―–ΨΩ÷γ“ΙΈ¬≤ν¥σ–Γ”κΜΦΗ–ΟΑ»Υ ΐΕύ…Ό÷°ΦδΒΡΙΊœΒΘ§ΥϊΟ«Ζ÷±πΒΫ
–ΤχœσΙέ≤β’Ψ”κ –“Ϋ‘Κ≥≠¬ΦΝΥ1÷Ν6‘¬ΖίΟΩ‘¬10Κ≈ΒΡ÷γ“ΙΈ¬≤ν«ιΩω”κ“ρΜΦΗ–ΟΑΕχΨΆ’οΒΡ»Υ ΐΘ§ΒΟΒΫ
»γœ¬Ή ΝœΘΚ
»’ΤΎ | 1‘¬10»’ | 2‘¬10»’ | 3‘¬10»’ | 4‘¬10»’ | 5‘¬10»’ | 6‘¬10»’ |
÷γ“ΙΈ¬≤ν | 10 | 11 | 13 | 12 | 8 | 6 |
ΨΆ’ο»Υ ΐ | 22 | 25 | 29 | 26 | 16 | 12 |
ΗΟΉέΚœ ΒΦυ―–ΨΩ–ΓΉι»ΖΕ®ΒΡ―–ΨΩΖΫΑΗ «ΘΚœ»¥”’βΝυΉι ΐΨί÷–―Γ»Γ2ΉιΘ§”Ο Θœ¬ΒΡ4Ήι ΐΨί«σœΏ–‘ΜΊΙιΖΫ≥ΧΘ§‘Ό”Ο±Μ―Γ»ΓΒΡ2Ήι ΐΨίΫχ––Φλ―ι.
Θ®1Θ©»τ―Γ»ΓΒΡ «1‘¬”κ6‘¬ΒΡΝΫΉι ΐΨίΘ§«κΗυΨί2÷Ν5‘¬ΖίΒΡ ΐΨίΘ§«σ≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ
ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() Θ°
Θ°
Θ®2Θ©»τ”…œΏ–‘ΜΊΙιΖΫ≥ΧΒΟΒΫΒΡΙάΦΤ ΐΨί”κΥυ―Γ≥ωΒΡΦλ―ι ΐΨίΒΡΈσ≤νΨυ≤Μ≥§Ιΐ2»ΥΘ§‘ρ»œΈΣΒΟΒΫΒΡœΏ–‘ΜΊΙιΖΫ≥Χ «άμœκΒΡΘ§ ‘Έ ΗΟ–ΓΉιΥυΒΟœΏ–‘ΜΊΙιΖΫ≥Χ «Ζώάμœκ?
≤ΈΩΦ ΐΨίΘΚ
![]()
![]() .
.
≤ΈΩΦΙΪ ΫΘΚΜΊΙι÷±œΏ![]() Θ§Τδ÷–
Θ§Τδ÷– .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®1©¹ ![]() Θ©ΒΡΕ®“ε”ρΈΣ[1Θ§+ΓόΘ©Θ§‘ρΚ· ΐy=
Θ©ΒΡΕ®“ε”ρΈΣ[1Θ§+ΓόΘ©Θ§‘ρΚ· ΐy= ![]() ΒΡΕ®“ε”ρΈΣ Θ°
ΒΡΕ®“ε”ρΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΐ‘≠ΒψΒΡΕ·÷±œΏl”κ‘≤![]() œύΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ§BΘ°
œύΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ§BΘ°
Θ®1Θ©«σœΏΕΈABΒΡ÷–ΒψMΒΡΙλΦΘCΒΡΖΫ≥ΧΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐkΘ§ ΙΒΟ÷±œΏLΘΚy=kΘ®x©¹4Θ©”κ«ζœΏC÷Μ”–“ΜΗωΫΜΒψΘΩ»τ¥φ‘ΎΘ§«σ≥ωkΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°

Θ®1Θ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τΤΫΟφ![]()
![]() ΤΫΟφ
ΤΫΟφ![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ100Οϊ―ß…ζΤΎ÷–ΩΦ ‘”οΈΡ≥…Φ®ΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ ΨΘ§Τδ÷–≥…Φ®Ζ÷Ήι«χΦδ «ΘΚ[50,60][60,70][70,80][80,90][90,100].

(1)«σΆΦ÷–aΒΡ÷ΒΘΜ
(2)ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΙάΦΤ’β100Οϊ―ß…ζ”οΈΡ≥…Φ®ΒΡΤΫΨυΖ÷ΘΜ
(3)»τ’β100Οϊ―ß…ζ”οΈΡ≥…Φ®Ρ≥–©Ζ÷ ΐΕΈΒΡ»Υ ΐΘ®xΘ©”κ ΐ―ß≥…Φ®œύ”ΠΖ÷ ΐΕΈΒΡ»Υ ΐΘ®yΘ©÷°±»»γœ¬±μΥυ ΨΘ§«σ ΐ―ß≥…Φ®‘Ύ[50Θ§90Θ©÷°ΆβΒΡ»Υ ΐ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±»ΐάβ÷υABC©¹A1B1C1÷–Θ§BC= ![]() Θ§AB=AC=AA1=1Θ§D «άβCC1…œΒΡ“ΜΒψΘ§P «ADΒΡ―”≥ΛœΏ”κA1C1ΒΡ―”≥ΛœΏΒΡΫΜΒψΘ§«“PB1ΓΈΤΫΟφBDA1 Θ°
Θ§AB=AC=AA1=1Θ§D «άβCC1…œΒΡ“ΜΒψΘ§P «ADΒΡ―”≥ΛœΏ”κA1C1ΒΡ―”≥ΛœΏΒΡΫΜΒψΘ§«“PB1ΓΈΤΫΟφBDA1 Θ° 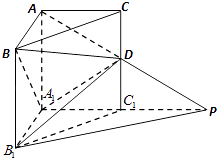
Θ®1Θ©«σ÷ΛΘΚCD=C1DΘΜ
Θ®2Θ©«σΕΰΟφΫ«A1©¹B1D©¹PΒΡΤΫΟφΫ«ΒΡ’ΐœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΒψP ««ζœΏy=x3©¹ ![]() x+
x+ ![]() …œΒΡ»Έ“β“ΜΒψΘ§ΒψP¥ΠΒΡ«–œΏ«ψ–±Ϋ«ΈΣΠΝΘ§‘ρΠΝΒΡ»Γ÷ΒΖΕΈßΈΣ Θ°
…œΒΡ»Έ“β“ΜΒψΘ§ΒψP¥ΠΒΡ«–œΏ«ψ–±Ϋ«ΈΣΠΝΘ§‘ρΠΝΒΡ»Γ÷ΒΖΕΈßΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=x3©¹9xΘ§Κ· ΐgΘ®xΘ©=3x2+aΘ°
Θ®1Θ©“―÷Σ÷±œΏl ««ζœΏy=fΘ®xΘ©‘ΎΒψΘ®0Θ§fΘ®0Θ©Θ©¥ΠΒΡ«–œΏΘ§«“l”κ«ζœΏy=gΘ®xΘ©œύ«–Θ§«σaΒΡ÷ΒΘΜ
Θ®2Θ©»τΖΫ≥ΧfΘ®xΘ©=gΘ®xΘ©”–»ΐΗω≤ΜΆ§ Β ΐΫβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com