
【题目】对于函数![]() 的定义域为
的定义域为![]() ,如果存在区间
,如果存在区间![]() ,同时满足下列条件:
,同时满足下列条件:
①![]() 在
在![]() 上是单调函数;
上是单调函数;
②当![]() 的定义域为
的定义域为![]() 时,值域也是
时,值域也是![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“
的“![]() 区间”.对于函数
区间”.对于函数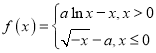
![]() .
.
(1)若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上存在“
上存在“![]() 区间”,求
区间”,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】边长为![]() 的等边三角形内任一点到三边距离之和为定值,则这个定值为
的等边三角形内任一点到三边距离之和为定值,则这个定值为![]() ;推广到空间,棱长为
;推广到空间,棱长为![]() 的正四面体内任一点到各面距离之和为___________________.
的正四面体内任一点到各面距离之和为___________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今有6个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有_____种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民月收入总额(工资、薪金等)不超过免征额的部分不必纳税,超过免征额的部分为全月应纳税所得额,个人所得税税款按税率表分段累计计算.为了给公民合理减负,稳步提升公民的收入水平,自2018年10月1日起,个人所得税免征额和税率进行了调整,调整前后的个人所得税税率表如下:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率 | 级数 | 全月应纳税所得额 | 税率 |
1 | 不超过1500元的部分 |
| 1 | 不超过3000元的部分 |
|
2 | 超过1500元至4500元的部分 |
| 2 | 超过3000元至12000元的部分 |
|
3 | 超过4500元至9000元的部分 |
| 3 | 超过12000元至25000元的部分 |
|
… | … | … | … | … | … |
(1)已知小李2018年9月份上交的税费是295元,10月份工资、薪金等税前收入与9月份相同,请帮小李计算一下税率调整后小李10月份的税后实际收入是多少?
(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100位不同层次员工的税前收入,并制成下面的频率分布直方图.
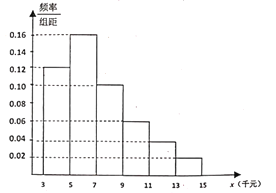
(i)请根据频率分布直方图估计该公司员工税前收入的中位数;
(ii)同一组中的数据以这组数据所在区间中点的值作代表,按调整后税率表,试估计小李所在的公司员工该月平均纳税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建极坐标系,直线
轴的非负半轴为极轴建极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)射线![]() 与圆C的交点为
与圆C的交点为![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)当![]() ,
,![]() 时,对任意的
时,对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 在两个不同零点
在两个不同零点![]() ,将关于
,将关于![]() 的不等式
的不等式![]() 的解集记为
的解集记为![]() .已知函数
.已知函数![]() 的最小值为
的最小值为![]() ,且函数
,且函数![]() 在
在![]() 上不存在最小值,求实数
上不存在最小值,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局公布的2013-2018年入境游客(单位:万人次)的变化情况,则下列结论错误的是( )

A.2014年我国入境游客万人次最少
B.后4年我国入境游客万人次呈逐渐增加趋势
C.这6年我国入境游客万人次的中位数大于13340万人次
D.前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com