
【题目】如图,在直三棱柱![]() 中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
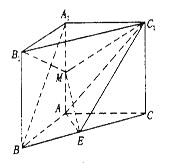
(Ⅰ)求证:A1B//平面AEC1;
(Ⅱ)在棱AA1上存在一点M,满足![]() ,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且cosC= ![]() .
.
(1)求B;
(2)设CM是角C的平分线,且CM=1,b=6,求cos∠BCM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小萌大学毕业后,家里给了她10万元,她想办一个“萌萌”加工厂,根据市场调研,她得出了一组毛利润![]() (单位:万元)与投入成本
(单位:万元)与投入成本![]() (单位:万元)的数据如下:
(单位:万元)的数据如下:
投入成本 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 |
毛利润 | 1.06 | 1.25 | 2 | 3.25 | 5 | 7.25 | 9.98 |
为了预测不同投入成本情况下的利润,她想在两个模型![]() ,
,![]() 中选一个进行预测.
中选一个进行预测.
(1)根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式,请你根据给定数据选出一个较好的函数模型进行预测(不必说明理由),并预测她投入8万元时的毛利润;
(2)若小萌准备最少投入2万元开办加工厂,请预测加工厂毛利润率![]() 的最大值,并说明理由.(
的最大值,并说明理由.(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y2=2px(p>0)焦点F的直线与抛物线交于A,B两点,作AC,BD垂直抛物线的准线l于C,D,其中O为坐标原点,则下列结论正确的是 . (填序号)
① ![]() ;
;
②存在λ∈R,使得 ![]() 成立;
成立;
③ ![]() =0;
=0;
④准线l上任意一点M,都使得 ![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣mx(m∈R).
﹣mx(m∈R).
(1)当m=0时,求函数f(x)的零点个数;
(2)当m≥0时,求证:函数f(x)有且只有一个极值点;
(3)当b>a>0时,总有 ![]() >1成立,求实数m的取值范围.
>1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有标号为![]() ,
,![]() ,
,![]() 的
的![]() 个小球,其中标号
个小球,其中标号![]() 的小球有
的小球有![]() 个,标号
个,标号![]() 的小球有
的小球有![]() 个,标号
个,标号![]() 的小球有
的小球有![]() 个,现从口袋中随机摸出
个,现从口袋中随机摸出![]() 个小球.
个小球.
(![]() )求摸出
)求摸出![]() 个小球标号之和为偶数的概率.
个小球标号之和为偶数的概率.
(![]() )用
)用![]() 表示摸出
表示摸出![]() 个小球的标号之和,写出
个小球的标号之和,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x).对任意的a,b∈R.满足:f(a+b)=f(a)f(b),当x>0时,有f(x)>1,其中f(1)=2.
(1)求f(0),f(﹣1)的值;
(2)判断该函数的单调性,并证明;
(3)求不等式f(x+1)<4的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条不同直线![]() 、
、![]() ,两个不同平面
,两个不同平面![]() 、
、![]() ,给出下列命题:
,给出下列命题:
①若![]() 垂直于
垂直于![]() 内的两条相交直线,则
内的两条相交直线,则![]() ⊥
⊥![]() ;
;
②若![]() ∥
∥![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;
内的所有直线;
③若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ;
;
④若![]()
![]()
![]() ,
,![]() ,则
,则![]() ⊥
⊥![]() ;
;
⑤若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ;
;
其中正确命题的序号是__________________.(把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com