
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 有共同的焦点,且离心率为
有共同的焦点,且离心率为![]() ,设
,设![]() 分别是
分别是![]() 为椭圆的上下顶点
为椭圆的上下顶点
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,当弦
,当弦![]() 的中点
的中点![]() 落在四边形
落在四边形![]() 内(含边界)时,求直线
内(含边界)时,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
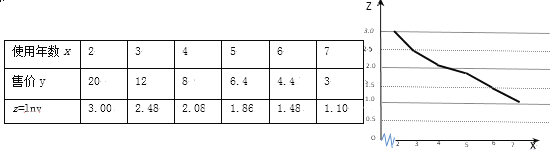
如图是z关于x的折线图:
(1)由折线图可以看出,可以用线性回归模型拟合z和x的关系,请用相关系数r加以说明(注:若相关系数︱r︱![]() 0.75,则认为两个变量相关程度较强);
0.75,则认为两个变量相关程度较强);
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?(![]() 小数点后面保留两位有效数字);
小数点后面保留两位有效数字);
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号的二手车时车辆的使用年限不得超过多少年?
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
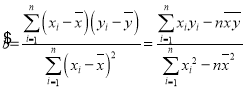 ,
,
参考数据: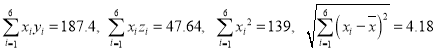
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中
(其中![]() ,m,n为常数)
,m,n为常数)
(1)当![]() 时,对
时,对![]() 有
有![]() 恒成立,求实数n的取值范围;
恒成立,求实数n的取值范围;
(2)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() 的零点为
的零点为![]() ,求所有满足
,求所有满足![]() 的整数k的和.
的整数k的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“斗拱”是中国古代建筑中特有的构件,从最初的承重作用,到明清时期集承重与装饰作用于一体.在立柱顶、额枋和檐檩间或构架间,从枋上加的一层层探出成弓形的承重结构叫拱拱与拱之间垫的方形木块叫斗.如图所示,是“散斗”(又名“三才升”)的三视图(三视图中的单位:分米),现计划用一块长方体的海南黄花梨木料加工成该散斗,则长方体木料的最小体积为( )立方分米.
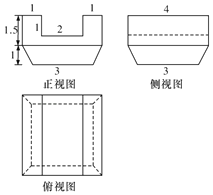
A.40B.![]() C.30D.
C.30D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在创建“全国文明卫生城”过程中,运城市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次),通过随机抽样,得到参加问卷调查的![]() 人的得分统计结果如表所示:.
人的得分统计结果如表所示:.
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)由频数分布表可以大致认为,此次问卷调查的得分![]() 似为这
似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求
人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求![]() ;
;
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) |
|
|
概率 |
|
|
现有市民甲参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:参考数据与公式:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 在圆内,在过点P所作的圆的所有弦中,弦长最小值为
在圆内,在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
(1)求实数a的值;
(2)若点M为圆外的动点,过点M向圆C所作的两条切线始终互相垂直,求点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com