
【题目】已知关于关于x的不等式ax2+bx+c<0的解集为(﹣∞,﹣2)∪(﹣ ![]() ,+∞),则不等式ax2﹣bx+c>0的解集为
,+∞),则不等式ax2﹣bx+c>0的解集为
【答案】( ![]() ,2)
,2)
【解析】解:关于x的不等式ax2+bx+c<0的解集为(﹣∞,﹣2)∪(﹣ ![]() ,+∞), ∴a<0,且﹣
,+∞), ∴a<0,且﹣ ![]() ,﹣2为方程ax2+bx+c=0的两根,
,﹣2为方程ax2+bx+c=0的两根,
∴﹣ ![]() +(﹣2)=﹣
+(﹣2)=﹣ ![]() ,且﹣
,且﹣ ![]() ×(﹣2)=
×(﹣2)= ![]() ;
;
∴b= ![]() a,c=a,
a,c=a,
∴不等式ax2﹣bx+c>0可化为ax2﹣ ![]() ax+a>0,
ax+a>0,
∴2x2﹣5x+2<0,
即(2x﹣1)(x﹣2)<0,
解得 ![]() <x<2,
<x<2,
∴不等式ax2﹣bx+c>0的解集为( ![]() ,2).
,2).
所以答案是:( ![]() ,2).
,2).
【考点精析】认真审题,首先需要了解解一元二次不等式(求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,证明:
两点,证明:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,坐标平面上一点P满足:
,坐标平面上一点P满足: ![]() 的周长为6,记点P的轨迹为
的周长为6,记点P的轨迹为![]() .抛物线
.抛物线![]() 以
以![]() 为焦点,顶点为坐标原点O.
为焦点,顶点为坐标原点O.
(Ⅰ)求![]() ,
, ![]() 的方程;
的方程;
(Ⅱ)若过![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,问在
两点,问在![]() 上且在直线
上且在直线![]() 外是否存在一点
外是否存在一点![]() ,使直线
,使直线![]() 的斜率依次成等差数列,若存在,请求出点
的斜率依次成等差数列,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x>0时,函数f(x)的解析式为![]() .
.
(1)求当x<0时函数f(x)的解析式;
(2)用定义证明f(x)在(0,+∞)上的是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点. (Ⅰ)求多面体ABCB′C′E的体积;
(Ⅱ)求异面直线C'E与CF所成角的余弦值.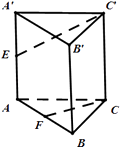
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品![]() 和
和![]() .这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
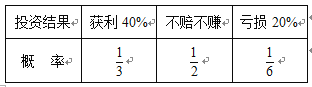
产品![]() (其中
(其中![]() )
)
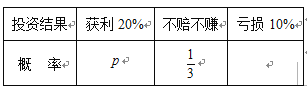
(Ⅰ)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于
进行投资,如果一年后他们中至少有一人获利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,点
,点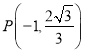 在椭圆
在椭圆![]() 上,
上, ![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 分别交于
分别交于![]() 两点.
两点.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 的面积为
的面积为![]() 为坐标原点,求直线
为坐标原点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当 ![]() 时,S为四边形
时,S为四边形
②截面在底面上投影面积恒为定值 ![]()
③不存在某个位置,使得截面S与平面A1BD垂直
④当 ![]() 时,S与C1D1的交点满足C1R1=
时,S与C1D1的交点满足C1R1= ![]()
其中正确命题的个数为 ( )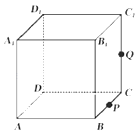
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com