
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
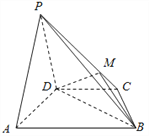
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
科目:高中数学 来源: 题型:
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
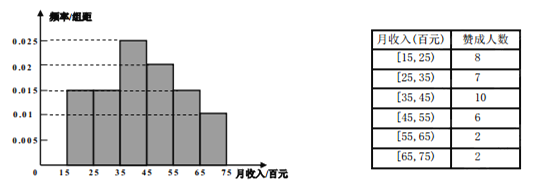
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 短轴顶点在圆
短轴顶点在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 方程;
方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究以
两点,试探究以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
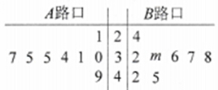
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,
轴上,![]() ,且对角线
,且对角线![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是直线
是直线![]() 上任意一点,过点
上任意一点,过点![]() 作点
作点![]() 的轨迹
的轨迹![]() 的两切线
的两切线![]() ,
,![]() 为切点,直线
为切点,直线![]() 是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图. 为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求a>b的概率;
(3)若a=1,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时,![]() 达到最值.
达到最值.
(只需写出结论)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1) 若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围;
(2) 已知函数f(x)=x2+2mx+3m+4.
① 若函数f(x)有且仅有一个零点,求实数m的值;
若函数f(x)有两个零点且两个零点均比-1大,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com