
 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 的期望
的期望 与方差
与方差 .
.| ξ | -1 | 0 | 1 |
| P |  | 1-2q[ | q2 |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:不详 题型:解答题
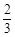 ,现种植这种种子4粒,求:
,现种植这种种子4粒,求: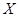 的分布列及平均数.
的分布列及平均数. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
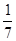 ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。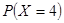 ;
;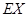 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 两个项目,投资
两个项目,投资 项目
项目 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析, 的分布列为:
的分布列为:
 项目
项目 万元,一年后获得的利润
万元,一年后获得的利润 (万元)与
(万元)与 项目产品价格的调整(价格上调或下调)有关, 已知
项目产品价格的调整(价格上调或下调)有关, 已知 项目产品价格在一年内进行
项目产品价格在一年内进行 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
. 项目产品价格的下调与一年后获得相应利润的关系如下表:
项目产品价格的下调与一年后获得相应利润的关系如下表: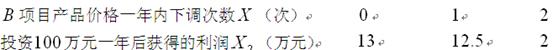
 的方差
的方差 ;
; 的分布列;
的分布列; ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目? ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com