
分析 由直线的倾斜及和斜率的关系,以及正切函数的值域可得.
解答 解:设直线x-ysinθ+1=0的倾斜角为α,
当$α=\frac{π}{2}$时,则sinθ=0,符合题意,
当$α≠\frac{π}{2}$时,sinθ≠0,
可得直线的斜率k=$tanα=\frac{1}{sinθ}∈(-∞,-1]∪[1,+∞)$,
又∵0<α<π,∴$\frac{π}{4}≤α<\frac{π}{2}$或$\frac{π}{2}<α≤\frac{3π}{4}$.
综上满足题意的倾斜角范围为:$[\frac{π}{4},\frac{3π}{4}]$
故答案为:$[\frac{π}{4},\frac{3π}{4}]$
点评 本题考查斜率的概念及正弦、正切函数的图象和值域,属基础题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
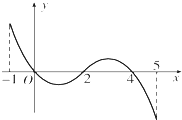 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
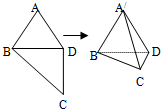 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com