
【题目】已知f(x)=e2x , g(x)=lnx+ ![]() ,对a∈R,b∈(0,+∞),使得f(a)=g(b),则b﹣a的最小值为 .
,对a∈R,b∈(0,+∞),使得f(a)=g(b),则b﹣a的最小值为 .
【答案】1+ ![]() ln2
ln2
【解析】解:∵f(x)=e2x , g(x)=lnx+ ![]() , ∴f﹣1(x)=
, ∴f﹣1(x)= ![]() lnx,g﹣1(x)=
lnx,g﹣1(x)= ![]() ,
,
令h(x)=g﹣1(x)﹣f﹣1(x)= ![]() ﹣
﹣ ![]() lnx,
lnx,
则b﹣a的最小值,即为h(x)的最小值,
∵h′(x)= ![]() ﹣
﹣ ![]() ,
,
令h′(x)=0,解得x= ![]()
∵当x∈(0, ![]() )时,h′(x)<0,当x∈(
)时,h′(x)<0,当x∈( ![]() ,+∞)时,h′(x)>0,
,+∞)时,h′(x)>0,
故当x= ![]() 时,h(x)取最小值1﹣
时,h(x)取最小值1﹣ ![]() ln
ln ![]() =1+
=1+ ![]() ln2,
ln2,
所以答案是:1+ ![]() ln2
ln2
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知向量m ![]() (sin
(sin ![]() ,1),
,1), ![]() =(1,
=(1, ![]() cos
cos ![]() ),函数f(x)=
),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)若f(α﹣ ![]() )=
)= ![]() ,求f(2α+
,求f(2α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
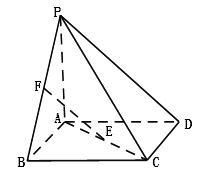
【题目】如图,四棱锥 ![]() 的底面
的底面 ![]() 为正方形,
为正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥 ![]() 的外接球的体积.
的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图圆柱高为 ![]() ,半径为
,半径为 ![]() ,不计厚度,单位:米),按计划容积为
,不计厚度,单位:米),按计划容积为 ![]() 立方米,且
立方米,且 ![]() ,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
(1)求y关于r的函数关系,并求其定义域;
(2)求建造费用最小时的 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣alnx+x(a∈R)
(Ⅰ)当a=1时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(Ⅱ)讨论函数y=f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 的部分图象如图所示.
的部分图象如图所示.
(1)求函数![]() 的解析式;
的解析式;
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 图象的一个对称轴为
图象的一个对称轴为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在第(2)问的前提下,求函数![]() 在
在![]() 上的单调区间.
上的单调区间.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|ax﹣1|.
(Ⅰ)若f(x)≤2的解集为[﹣6,2],求实数a的值;
(Ⅱ)当a=2时,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤7﹣3m成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com