
����Ŀ��Ϊ��Ӧ��������ġ����ڴ�ҵ�����ڴ��¡��ĺ���,С��ͬѧ��ѧ��ҵ��,����������ѧרҵ����������ҵ�������г�����,����ijС�͵��Ӳ�Ʒ��Ͷ����̶��ɱ�Ϊ5��Ԫ��ÿ������![]() ���������Ͷ�������ɱ�Ϊ
���������Ͷ�������ɱ�Ϊ![]() ��Ԫ����
��Ԫ����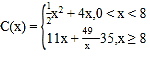 ��ÿ����Ʒ�ۼ�Ϊ10Ԫ�����г�����,�����IJ�Ʒ������ȫ�����ꡣ
��ÿ����Ʒ�ۼ�Ϊ10Ԫ�����г�����,�����IJ�Ʒ������ȫ�����ꡣ
(1)д��������![]() (��Ԫ)���������
(��Ԫ)���������![]() (���)�ĺ�������ʽ��
(���)�ĺ�������ʽ��
(ע:������=����������-�̶��ɱ�-�����ɱ�)
(2)�����Ϊ�������ʱ��С������һ��Ʒ�������������������?��������Ƕ���?
���𰸡���1��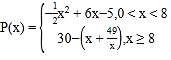 ��
��
��2���������Ϊ8���ʱ��С������һ��Ʒ��������������������������Ϊ![]() ��Ԫ��
��Ԫ��
��������
��1����Ϊÿ����Ʒ�ۼ�Ϊ10ԭ����![]() �����Ʒ��������Ϊ
�����Ʒ��������Ϊ![]() ��Ԫ��������������ۣ���
��Ԫ��������������ۣ���![]() ʱ����
ʱ����![]() ʱ���ֱ��������������ȥ�ɱ��ɵó�������
ʱ���ֱ��������������ȥ�ɱ��ɵó�������![]() (��Ԫ)���������
(��Ԫ)���������![]() (���)�ĺ�������ʽ����2����
(���)�ĺ�������ʽ����2����![]() ʱ���ɶ��κ��������ʿɵ�
ʱ���ɶ��κ��������ʿɵ�![]() ȡ�����ֵ
ȡ�����ֵ![]() ����
����![]() ʱ��
ʱ�� ![]() ȡ�����ֵ
ȡ�����ֵ![]() ����
����![]() �ɵý��.
�ɵý��.
��1����Ϊÿ����Ʒ�ۼ�Ϊ10Ԫ����![]() �����Ʒ��������Ϊ
�����Ʒ��������Ϊ![]() ��Ԫ��
��Ԫ��
������ã�
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]() ��
��
����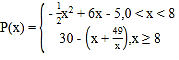
��2����![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]() ȡ�����ֵ
ȡ�����ֵ![]()
��![]() ʱ��
ʱ��![]() ������
������![]() ��������
��������
��![]() ʱ��
ʱ��![]() ȡ�����ֵ
ȡ�����ֵ![]() ����Ϊ
����Ϊ![]()
�ʵ������Ϊ8���ʱ��С������һ��Ʒ��������������������������Ϊ![]() ��Ԫ
��Ԫ


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС����ѧ���ͽ�ʦ��ɣ���Ա����ͬʱ��������������������������������Ů����������Ů���������ڽ�ʦ�������۽�ʦ�������������������������ʣ�
��1������ʦ����Ϊ4����Ů�����������ֵΪ���٣�
��2����С����������СֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,���![]() Ϊ��Բ
Ϊ��Բ![]() ���ҽ��㣬Բ
���ҽ��㣬Բ![]() ��
��![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ��
��![]() ���㣬����Բ
���㣬����Բ![]() �ڵ�
�ڵ�![]() ���㣬��֪��
���㣬��֪��![]() ʱ��
ʱ��![]()
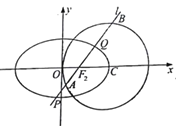
��1������Բ![]() �ķ���.
�ķ���.
��2����![]() ʱ����
ʱ����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��A1B1C1D1�У�DA��DC��2��![]() ��E��C1D1���е㣬F��CE���е㣮
��E��C1D1���е㣬F��CE���е㣮
��1����֤��EA��ƽ��BDF��
��2����֤��ƽ��BDF��ƽ��BCE��
��3��������D��EB��C������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˿��˼ף��������ŵĹ�����������������50λ��������50λ������������ŵ����֣�����Խ�߱������������Խ�ߣ������ƾ�Ҷͼ���£�

��1���ֱ���Ƹ��е�����Լף������������ֵ���λ����
��2���ֱ���Ƹ��е�����Լף��������ŵ����ָ���90�ĸ��ʣ�
��3�����ݾ�Ҷͼ�������е�����Լף��������ŵ����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͭ���г�����ڽ���6��1��������˼ۣ����мƼ۱��ǣ�·����2.5km���ڣ���2.5km������7Ԫ��ȡ������2.5km���·�̰�1.9Ԫkm��ȡ��������8km���·�������50%�ķ��շѣ�������Ϊ![]() Ԫ��.
Ԫ��.
��1����ij�˿ʹ��һ�γ���ķ���![]() ����λ��Ԫ����ʾΪ�г�x��
����λ��Ԫ����ʾΪ�г�x��![]() ����λ��km���ķֶκ�����
����λ��km���ķֶκ�����
��2��ij�˿͵��г�Ϊ16km�������ȳ�һ�������ʻ8km���ٻ�����һ�������������г̣����ʣ����������Ƿ��ֻ��һ��������ȫ���г̸�ʡǮ?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC����a=7��b=8��cosB= �C![]() ��
��
����������A��
��������AC���ϵĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���![]() ����
����![]() ��
�� ![]() ����
����![]() ��
��![]() ͼ��Ľ�������Ϊ
ͼ��Ľ�������Ϊ![]() ����
����![]() ����
����![]() ����СֵΪ____��
����СֵΪ____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com