
【题目】四边形![]() 中,
中,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,如图(1),将其沿
,如图(1),将其沿![]() 折起使得平面
折起使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图(2).
,如图(2).
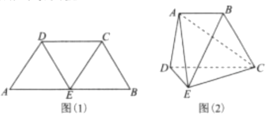
(1)证明:图(2)中的![]() 四点共面;
四点共面;
(2)求图(2)中平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)分析翻折后,取DE,CE中点M,N,连接MN,AM,BN利用平面几何知识证明![]() ,
,![]() ,进而得到
,进而得到![]() ,则A,B,C,D四点共面;
,则A,B,C,D四点共面;
(2)以N为原点建立如图所示空间直角坐标系,根据等量关系写出A,C,D,E,N五点坐标,求出平面BCE和平面ACE的法向量,将两个平面所成的锐二面角转化为法向量所成角的余弦值来求解.
(1)翻折前,由题意AB=2CD=2AD=2BC=2,E为AB的中点,可得AE=EB=BC=CD=DA=1,又AB![]() CD,
CD,![]() ,
,![]() ,则可得AD=CE=1,同理DE=BC=1,
,则可得AD=CE=1,同理DE=BC=1,
翻折后,取DE,CE中点M,N,连接MN,AM,BN,如图所示:
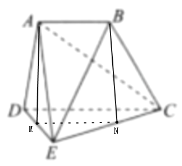
则MN![]() CD,在△ADE和△BCE内:AM
CD,在△ADE和△BCE内:AM![]() DE,BN
DE,BN![]() CE,
CE,
由平面![]() 平面
平面![]() , 平面
, 平面![]() 平面
平面![]() =DE,
=DE,
![]() AM
AM![]() 平面
平面![]() ,同理BN
,同理BN![]() 平面
平面![]() ,
,![]() AM
AM![]() BN,由题意等量关系易得AM
BN,由题意等量关系易得AM![]() BN,可得四边形ABNM为平行四边形,所以AB
BN,可得四边形ABNM为平行四边形,所以AB![]() NM,由MN
NM,由MN![]() CD得AB
CD得AB![]() CD,所以翻折后A,B,C,D四点共面.
CD,所以翻折后A,B,C,D四点共面.
(2)翻折后,以N为原点,NB所在的直线为![]() 轴,ND所在的直线为
轴,ND所在的直线为![]() 轴,NE所在的直线为
轴,NE所在的直线为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
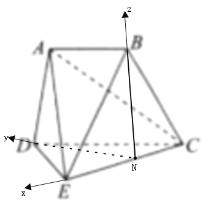
则有如下坐标:A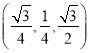 ,C
,C![]() ,D
,D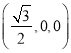 ,E
,E![]() ,N
,N![]() ,则
,则 ,
,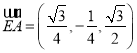 ,
,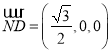 ,设平面
,设平面![]() 的法向量
的法向量![]() ,由
,由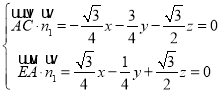 令
令![]() ,联立可解得
,联立可解得![]() ,所以
,所以![]() ,又平面
,又平面![]() 的法向量为
的法向量为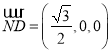
所以由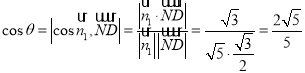 ,即平面BCE和平面ACE所成的锐二面角的余弦值为
,即平面BCE和平面ACE所成的锐二面角的余弦值为![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线l过定点
,直线l过定点![]() .
.
(1)若直线l与圆C相切,求直线l的方程;
(2)若直线l与圆C相交于P,Q两点,求![]() 的面积的最大值,并求此时直线l的方程.
的面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列命题:①对于实数![]() ,若
,若![]() ,则
,则![]() ;②
;②![]() 是
是![]() 的充分而不必要条件;③在(增减算法统宗》中有这样一则故事: 三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关“则此人第二天走了九十六里路;④设函数
的充分而不必要条件;③在(增减算法统宗》中有这样一则故事: 三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关“则此人第二天走了九十六里路;④设函数![]() 的定又域为R,若存在常数:
的定又域为R,若存在常数:![]() ,使
,使![]() 对一切实数x均成立、则称
对一切实数x均成立、则称![]() 为“倍约束函数,所以函数
为“倍约束函数,所以函数![]() 为"倍约束函数”其中所有真命题的序号是_____________.
为"倍约束函数”其中所有真命题的序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
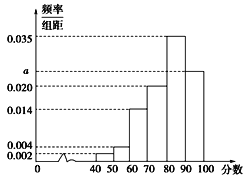
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() 分别为椭圆C:
分别为椭圆C:![]() 的左右焦点,椭圆
的左右焦点,椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上,不在
在椭圆C上,不在![]() 轴上的动点P与动点Q关于原点O对称,且四边形
轴上的动点P与动点Q关于原点O对称,且四边形![]() 的周长为
的周长为![]() .
.
(1)求动点P的轨迹方程;
(2)在动点P的轨迹上有两个不同的点M![]() ,N
,N![]() ,线段MN的中点为G,已知点
,线段MN的中点为G,已知点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值,并判断此时ΔOMN的形状.
的最大值,并判断此时ΔOMN的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com