
【题目】设函数![]() ①若
①若![]() ,则
,则![]() 的零点有_____个;②若
的零点有_____个;②若![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是________.
的取值范围是________.
【答案】![]()
![]()
【解析】
①根据题意,若a=1,f(x)![]() ,分段分析函数的零点,综合即可得答案;
,分段分析函数的零点,综合即可得答案;
②根据题意,由函数的解析式分析可得a≥0,在同一坐标系中作出y=﹣|x|(x+2)与y=lnx的图象,结合图象分析可得若f(x)的值域为[﹣1,+∞),必有![]() ,解可得a的取值范围,即可得答案.
,解可得a的取值范围,即可得答案.
解:①,根据题意,若a=1,f(x)![]() ,
,
当x>1时,f(x)=lnx,f(x)=0即lnx=0,无解;
当x≤1时,f(x)=﹣|x|(x+2),若f(x)=0即﹣|x|(x+2)=0,
解可得x=0或﹣2,
则f(x)=0有2解,即x=0或﹣2,即f(x)有2个零点;
②,根据题意,![]() ,必有a≥0,
,必有a≥0,
y=﹣|x|(x+2)![]() ,y=lnx,其图象如图:
,y=lnx,其图象如图:
若f(x)的值域为[﹣1,+∞),必有![]() ,
,
解可得:![]() a
a![]() 1,即a的取值范围为[
1,即a的取值范围为[![]() ,
,![]() 1];
1];
故答案为:①、2,②、[![]() ,
,![]() 1].
1].


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: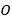 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级学生会主席团有共有![]() 名同学组成,其中有
名同学组成,其中有![]() 名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]()
![]() ,过抛线
,过抛线![]() 上一点
上一点![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于A、B两点,分别交抛物线于E、F两点,圆心点
相切于A、B两点,分别交抛物线于E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
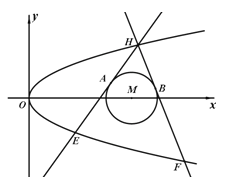
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)当![]() 的角平分线垂直x轴时,求直线EF的斜率;
的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,已知公差
中,已知公差![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求![]() .
.
【答案】(1)![]() ;(2)100
;(2)100
【解析】试题分析:(1)根据题意![]() ,
, ![]() ,
, ![]() 成等比数列得
成等比数列得![]() 得
得![]() 求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得
求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]()
![]()
![]()
![]() 计算 即可得出结论
计算 即可得出结论
解析:(1)由题意可得,则![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(2)由(1)得![]() 时,
时,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
∴![]() .
.
点睛:对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决,对于第二问前n项的绝对值的和问题,首先要找到数列由多少正数项和负数项,进而找到绝对值所影响的项,然后在求解即可得结论
【题型】解答题
【结束】
18
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
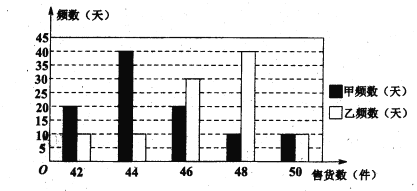
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为
,左顶点为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 和
和![]() ,分别交直线
,分别交直线![]() 于
于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在首届中国国际商品博览会期间,甲、乙、丙三家供货公司各签订了两个供货合同,已知这三家公司供货合同中金额分别是300万元和600万元、300万元和900万元、600万元和900万元,甲看了乙的供货合同说:“我与乙的供货合同中金额相同的合同不是600万元”,乙看了丙的供货合同说:“我与丙的供货合同中金额相同的合同不是300万元”,丙说:“我的两个供货合同中金额之和不是1500万元”,则甲签订的两个供货合同中金额之和是( )
A.900万B.1500万元C.不能确定D.1200万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是正整数.在一个十进制
是正整数.在一个十进制![]() 位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的
位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的![]() 位数的个数.
位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,记弦
两点,记弦![]() 的中点为
的中点为![]() ,点
,点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com