
【题目】截止到1999年底,我国人口约为13亿,若今后能将人口平均增长率控制在1%,经过x年后,我国人口为y(单位:亿).
(1)求y与x的函数关系式y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数,并指出函数增减的实际意义.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:
(1)由题意对每年的人数进行求解,然后归纳可得函数的解析式为y=f(x)=13×(1+1%)x;
(2)结合实际问题的应用范围可得函数的定义域为x∈N*;
(3)函数的底数大于1,则函数为增函数,其实际意义为只要递增率为正数,随着时间的推移,人口的总数总在增长.
试题解析:
(1)1999年底人口数:13亿.经过1年,2000年底人口数:13+13×1%=13×(1+1%)亿.经过2年,2001年底人口数:13×(1+1%)+13×(1+1%)×1%=13×(1+1%)2亿.经过3年,2002年底人口数:13×(1+1%)2+13×(1+1%)2×1%=13×(1+1%)3亿…
∵经过年数与(1+1%)的指数相同,∴经过x年后人口数为13×(1+1%)x亿,∴y=f(x)=13×(1+1%)x.
(2)∵此问题以年作为单位时间,∴x∈N*是此函数的定义域.
(3)y=f(x)=13×(1+1%)x.∵1+1%>1,13>0,∴y=f(x)=13×(1+1%)x是增函数,
即只要递增率为正数,随着时间的推移,人口的总数总在增长.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-2ax+2+b(a≠0)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-2mx在[2,4]上单调,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.

(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=1.1x,g(x)=ln x+1,h(x)=x![]() 的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
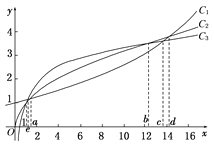
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为(![]() ,
,![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求这条曲线的函数解析式;
(2)写出函数的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com