
【题目】(2017·安徽名校阶段性测试)如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径CE=9.
(1)求证:平面ABE⊥平面ADE;
(2)求五面体ABCDE的体积.
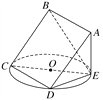
【答案】(1)见解析(2)![]()
【解析】试题分析:(1) 先由线面垂直性质定理得AE⊥CD. 再由圆的性质得CD⊥DE,由线面垂直判定定理得CD⊥平面ADE. 最后根据平行得AB⊥平面ADE.,由面面垂直判定定理得结论( 2)先将五面体分割成两个三棱锥B-ADE和B-CDE,两个三棱锥的高为AB,AE,最后代入锥体体积公式即得结果
试题解析:解:(1)证明:∵AE垂直于圆O所在平面,CD圆O所在平面,∴AE⊥CD.
又CD⊥DE,AE∩DE=E,AE平面ADE,DE平面ADE,
∴CD⊥平面ADE.
在正方形ABCD中,CD∥AB,
∴AB⊥平面ADE.
又AB平面ABE,
∴平面ABE⊥平面ADE.
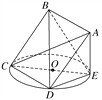
(2)连接AC,BD,设正方形ABCD的边长为a,则AC=![]() a,
a,
又AC2=CE2+AE2=90,
∴a=3![]() ,DE=6,
,DE=6,
∴VBADE=![]() BA·S△ADE
BA·S△ADE
=![]() ×3
×3![]() ×
×![]() =9
=9![]() .
.
又AB∥CD,CD平面CDE,
∴点B到平面CDE的距离等于点A到平面CDE的距离,即AE,
∴VBCDE=![]() AE·S△CDE=
AE·S△CDE=![]() ×3×
×3×![]() =9
=9![]() ,
,
故VABCDE=VBCDE+VBADE=18![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校初三年级有![]() 名学生,随机抽查了
名学生,随机抽查了![]() 名学生,测试
名学生,测试![]() 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )

A. 该校初三年级学生![]() 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为![]() 次
次
B. 该校初三年级学生![]() 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为![]() 次
次
C. 该校初三年级学生![]() 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过![]() 次的人数约有
次的人数约有![]() 人
人
D. 该校初三年级学生![]() 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于![]() 次的人数约为
次的人数约为![]() 人.
人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y-a)2=4,点A(1,0).
(1)当过点A的圆C的切线存在时,求实数a的取值范围;
(2)设AM、AN为圆C的两条切线,M、N为切点,当MN=![]() 时,求MN所在直线的方程.
时,求MN所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面四个类比结论:
①实数a,b,若ab=0,则a=0或b=0;类比复数z1,z2,若z1z2=0,则z1=0或z2=0.
②实数a,b,若ab=0,则a=0或b=0;类比向量a,b,若a·b=0,则a=0或b=0.
③实数a,b,有a2+b2=0,则a=b=0;类比复数z1,z2,有z+z=0,则z1=z2=0.
④实数a,b,有a2+b2=0,则a=b=0;类比向量a,b,若a2+b2=0,则a=b=0.
其中类比结论正确的个数是( )
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
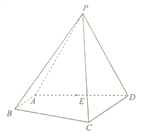
【题目】如图,在四棱锥![]() 中,
中, ![]() 是等边三角形,
是等边三角形, ![]() 为
为![]() 的中点,四边形
的中点,四边形![]() 为直角梯形,
为直角梯形, ![]()
![]()
![]()
![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过
过![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)设点![]() 在椭圆
在椭圆![]() 上.试问直线
上.试问直线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. 若命题![]() “
“![]() ,
, ![]() ”,则命题
”,则命题![]() 的否定为“
的否定为“![]() ,
, ![]() ”
”
C. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
D. “![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 互为垂直”的充要条件
互为垂直”的充要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com