分析:①x∈(-2,0)时,考察x
2+2x的函数值,即可判断函数f(x)的值的正负;②利用导数研究函数的单调性,先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间.利用②的结论结合函数的最值,研究函数的图象特征,从而得出③函数f(x)的图象不经过第四象限;④f(x)=
有且只有三个实数解.
解答: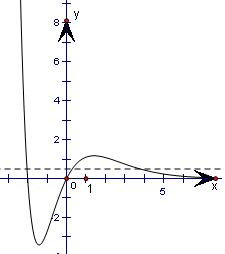
解:①x∈(-2,0)时,x
2+2x=x(x+2)<0,而e
-x>0,
∴f(x)<0,故①正确;
②∵f′(x)=-e
-x(x
2+2x)+e
-x(2x+2)=-e
-x(x
2-2),
∴f(x)的单调递增区间为(-
,
),单调递减区间为(-∞,-
),(
,+∞).
∴x∈(-1,1)时,f(x)单调递增.②正确,
又当x=
时,函数取得最大值(2+2
)e
->0.5,
当x=-
时,函数取得最大值(2-2
)e
<-3,
当x=0时,函数取值0,当x>0时,f(x)>0.
根据函数的单调性及特殊函数值,画出函数f(x)的图象,如图所示,则③函数f(x)的图象不经过第四象限;正确;
④f(x)=
有且只有三个实数解;正确.
故答案为:①、②、③、④.
点评:本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想.属于基础题.

 解:①x∈(-2,0)时,x2+2x=x(x+2)<0,而e-x>0,
解:①x∈(-2,0)时,x2+2x=x(x+2)<0,而e-x>0,
