【题目】在一个不透明的口袋中装有大小、形状完全相同的
个小球，将它们分别编号为
，
，
，…，，甲、乙、丙三人从口袋中依次各抽出个小球．甲说：我抽到了编号为的小球，乙说：我抽到了编号为
的小球，丙说：我没有抽到编号为的小球．已知甲、乙、丙三人抽到的个小球的编号之和都相等，且甲、乙、丙三人的说法都正确，则丙抽到的个小球的编号分别为________________．
【答案】
，
，
.
【解析】
利用等差数列求和公式求出所有球的编号的和，得到每个人抽出三个球的编号和，可得甲抽到的另外两个小球的编号和为6，乙抽到的另外两个小球的编号和为7，分类讨论，排除、验证即可得结果.
因为甲、乙、丙三人抽到的个小球的编号之和都相等，所以每个人抽到的个小球的编号之和为
．设甲抽到的另外两个小球的编号分别为
，
，乙抽到的另外两个小球的编号分别为
，
，则
，
，所以，的取值只有
与，
与
两种情况．当甲抽到编号为与的小球时，由可知乙抽到编号为与的小球，与丙没有抽到编号为的小球矛盾，所以甲抽到编号为与的小球，由可知乙抽到编号为与6的小球，则丙抽到的个小球的编号分别为，，,故答案为，，．
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥V－ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC，O，M分别为AB，VA的中点．
(1)求证：VB∥平面MOC；
(2)求证：平面MOC⊥平面VAB；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，
平面
.
（1）证明：
平面
；
（2）过点
作一平行于平面
的截面，画出该截面，说明理由，并求夹在该截面与平面之间的几何体的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一个口袋中装有n个红球(n≥1且n∈N+)和2个白球,从中有放回地连续摸三次,每次摸出2个球,若2个球颜色不同则为中奖,否则不中奖.
(1)当n=3时,设三次摸球中中奖的次数为X,求随机变量X的分布列;
(2)记三次摸球中恰有两次中奖的概率为P,求当n取多少时,P的值最大.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】基于移动网络技术的共享单车被称为“新四大发明”之一，短时间内就风靡全国，给人们带来新的出行体验，某共享单车运营公司的市场研究人员为了了解公司的经营状况，对公司最近6个月的市场占有率
进行了统计，结果如下表：
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
（1）请用相关系数说明能否用线性回归模型拟合
与月份代码
之间的关系.如果能，请计算出关于的线性回归方程，如果不能，请说明理由；
（2）根据调研数据，公司决定再采购一批单车扩大市场，从成本1000元/辆的
型车和800元/辆的
型车中选购一种，两款单车使用寿命频数如下表：
| 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算，平均每辆单车每年能为公司带来500元的收入，不考虑除采购成本以外的其它成本，假设每辆单车的使用寿命都是整数年，用频率估计每辆车使用寿命的概率，以平均每辆单车所产生的利润的估计值为决策依据，如果你是公司负责人，会选择哪款车型？
参考数据：
，
，
，
.
参考公式：相关系数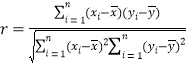
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两个焦点分别为
，离心率为
，过
的直线
与椭圆
交于
两点，且
的周长为
（1）求椭圆的方程；
（2）若直线
与椭圆分别交于
两点，且
，试问点
到直线
的距离是否为定值，证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业生产A、B两种产品，根据市场调查，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的平方根成正比，其关系如图2(注：单位是万元).
图1 图2
（1）若A、B两种产品的利润表示为投资的函数分别为
、
，求出它们的表达式并注明定义域；
（2）现企业有20万元资金全部投入A、B两种产品的生产，问：怎样分配这20万元资金，能使获得的利润最大，其最大利润是多少万元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
