【题目】假设有5个条件类似的女孩（把她们分别记为A，B，C，D， E）应聘秘书工作，但只有2个秘书职位，因此5个人中只有2人能被录用.如果5个人被录用的机会相等，分别计算下列事件的概率；
（1）女孩A得到一个职位；
（2）女孩A和B各得到一个职位；
（3）女孩A或B得到一个职位.
初中学业考试导与练系列答案科目：高中数学 来源： 题型：
【题目】如图，三棱柱
中，四边形
为菱形，
，平面
平面
，
在线段
上移动，
为棱
的中点.
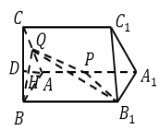
（1）若为线段的中点，
为
中点，延长
交
于
，求证：
平面
；
（2）若二面角
的平面角的余弦值为
，求点到平面
的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示的茎叶图记录了华润万家在渭南城区甲、乙连锁店四天内销售情况的某项指标统计：
（I）求甲、乙连锁店这项指标的方差，并比较甲、乙该项指标的稳定性；
（Ⅱ）每次都从甲、乙两店统计数据中随机各选一个进行比对分析，共选了3次（有放回选取）．设选取的两个数据中甲的数据大于乙的数据的次数为
，求的分布列及数学期望
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个盒子中装有标号为1,2,3,4,5的5张标签，随机地依次选取两张标签，根据下列条件求两张标签上的数字为相等整数的概率；
（1）标签的选取是不放回的；
（2）标签的选取是有放回的.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线．当t∈(0,14]时，曲线是二次函数图象的一部分，当t∈[14,40]时，曲线是函数
（
且
）图象的一部分．根据专家研究，当注意力指数p大于等于80时听课效果最佳．
(1)试求
的函数关系式；
(2)一道数学难题，讲解需要22分钟，问老师能否经过合理安排在学生听课效果最佳时讲完？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产某种型号的电视机零配件，为了预测今年
月份该型号电视机零配件的市场需求量，以合理安排生产，工厂对本年度
月份至
月份该型号电视机零配件的销售量及销售单价进行了调查，销售单价
（单位：元）和销售量
（单位：千件）之间的组数据如下表所示：
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
（1）根据1至月份的数据，求关于的线性回归方程（系数精确到
）；
（2）结合（1）中的线性回归方程，假设该型号电视机零配件的生产成本为每件
元，那么工厂如何制定月份的销售单价，才能使该月利润达到最大（计算结果精确到
）？
参考公式：回归直线方程
，其中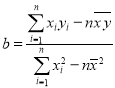
.
参考数据：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某品牌计算机售后保修期为1年，根据大量的维修记录资料，这种品牌的计算机在使用一年内需要维修1次的占15%，需要维修2次的占6%，需要维修3次的占4%.
（1）某人购买了一台这个品牌的计算机，设
=“一年内需要维修k次”，k=0,1,2,3,请填写下表：
事件 |
|
|
|
|
概率 |
事件
是否满足两两互斥？是否满足等可能性？
（2）求下列事件的概率：
①A=“在1年内需要维修”;
②B=“在1年内不需要维修”；
③C=“在1年内维修不超过1次”.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面内点
到点
的距离和到直线
的距离之比为
，若动点P的轨迹为曲线C．
（I）求曲线C的方程；
（II）过F的直线
与C交于A，B两点，点M的坐标为
设O为坐标原点.证明：
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
