
已知函数f(x)=ln x+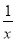 -1.
-1.
(1)求函数f(x)的单调区间;
(2)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-1练习卷(解析版) 题型:选择题
某几何体的三视图如图所示,则该几何体的体积为( ).

A.16+8π B.8+8π C.16+16π D.8+16π
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-1练习卷(解析版) 题型:填空题
函数y=tan ωx(ω>0)与直线y=a相交于A,B两点,且|AB|最小值为π,则函数f(x)=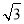 sin ωx-cos ωx的单调增区间是________.
sin ωx-cos ωx的单调增区间是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:选择题
函数y=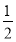 x2-ln x的单调减区间是 ( ).
x2-ln x的单调减区间是 ( ).
A.(-1,1] B.(0,1] C.[1,+∞) D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(解析版) 题型:选择题
设函数f(x)=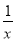 ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
A.x1+x2>0,y1+y2>0
B.x1+x2<0,y1+y2>0
C.x1+x2>0,y1+y2<0
D.x1+x2<0,y1+y2<0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-1练习卷(解析版) 题型:填空题
已知函数f(x)=e|x-a|(a为常数).若f(x)在区间[1,+∞)上是增函数,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(解析版) 题型:解答题
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=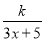 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-2练习卷(解析版) 题型:选择题
设x,y∈R,向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,则|a+b|= ( ).
A.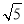 B.
B. 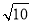 C.2
C.2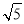 D.10
D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟1-7练习卷(解析版) 题型:选择题
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( ).
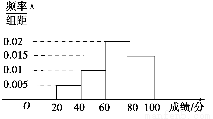
A.45 B.50 C.55 D.60
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com