
【题目】过圆![]() 上的点
上的点![]() 作圆
作圆![]() 的切线,过点
的切线,过点![]() 作切线的垂线
作切线的垂线![]() ,若直线
,若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() .
.
(1)求直线![]() 与抛物线
与抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 的准线上,且
的准线上,且![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() .
.![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)利用斜率求得过![]() 点的切线方程,由此得到垂线
点的切线方程,由此得到垂线![]() 的斜率,再由点斜式得到直线
的斜率,再由点斜式得到直线![]() 的方程,令
的方程,令 ![]() 可求得焦点
可求得焦点![]() 的坐标,由此得出抛物线
的坐标,由此得出抛物线![]() 的方程.(2)联立方程组求得
的方程.(2)联立方程组求得![]() 两点的坐标.设出点
两点的坐标.设出点![]() 的坐标,利用向量的数量积求得
的坐标,利用向量的数量积求得![]() 点的坐标,利用弦长公式和点到直线的距离公式得出面积.
点的坐标,利用弦长公式和点到直线的距离公式得出面积.
【试题解析】
(1)过点![]() 且与圆
且与圆![]() 相切的直线方程为
相切的直线方程为![]() ,
,
斜率为![]() ,故直线
,故直线![]() 的斜率为
的斜率为![]() ,故直线
,故直线![]() 的方程为:
的方程为: ![]() ,
,
即![]() .
.
令![]() ,可得
,可得![]() ,故
,故![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ;
;
(2)由 可得
可得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
点![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
, ![]() ,
,
则![]() ,解之得
,解之得![]() 或
或![]() ,
,
∴![]()
![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为 ,故
,故![]() 或
或![]() ,
,
当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C:![]() +
+![]() =1 (a>b>0)的离心率是
=1 (a>b>0)的离心率是![]() ,抛物线E:x2=2y的焦点F是C的一个顶点.
,抛物线E:x2=2y的焦点F是C的一个顶点.

(1)求椭圆C的方程;
(2)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的两点A,B,线段AB的中点为D.直线OD与过P且垂直于x轴的直线交于点M.
①求证:点M在定直线上;
②直线l与y轴交于点G,记△PFG的面积为S1,△PDM的面积为S2,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前,网购已成为现代大学生的时尚。某大学学生宿舍4人参加网购,约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有1人去淘宝网购物的概率;
(2)用![]() 分别表示这4个人中去淘宝网和京东商城购物的人数,记
分别表示这4个人中去淘宝网和京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区![]() 年该农产品的产量;
年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 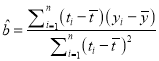 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大型水上乐园内有一块矩形场地![]() 米,
米, ![]() 米,以
米,以![]() 为直径的半圆
为直径的半圆![]() 和半圆
和半圆![]() (半圆在矩形
(半圆在矩形![]() 内部)为两个半圆形水上主题乐园,
内部)为两个半圆形水上主题乐园, ![]() 都建有围墙,游客只能从线段
都建有围墙,游客只能从线段![]() 处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着
处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着![]() 修建不锈钢护栏,沿着线段
修建不锈钢护栏,沿着线段![]() 修建该主题乐园大门并设置检票口,其中
修建该主题乐园大门并设置检票口,其中![]() 分别为
分别为![]() 上的动点,
上的动点, ![]() ,且线段
,且线段![]() 与线段
与线段![]() 在圆心
在圆心![]() 和
和![]() 连线的同侧.已知弧线部分的修建费用为
连线的同侧.已知弧线部分的修建费用为![]() 元/米,直线部门的平均修建费用为
元/米,直线部门的平均修建费用为![]() 元/米.
元/米.

(1)若![]() 米,则检票等候区域(其中阴影部分)面积为多少平方米?
米,则检票等候区域(其中阴影部分)面积为多少平方米?
(2)试确定点![]() 的位置,使得修建费用最低.
的位置,使得修建费用最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱台![]() 的三视图与直观图如图所示.
的三视图与直观图如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:

(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为
以上的把握认为
“桔柚直径与所在基地有关”?

(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表):
(同一组数据用该区间的中点值作代表):
(3)经计算,甲基地的500个桔柚直径的样本方差![]() ,乙基地的500个桔柚直径的样本方差
,乙基地的500个桔柚直径的样本方差![]() ,,并且可认为优质品率较高的基地采摘的桔柚直径
,,并且可认为优质品率较高的基地采摘的桔柚直径![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .由优质品率较高的种植基地的抽样数据,估计该基地采摘的桔柚中,直径不低于86.78亳米的桔柚在总体中所占的比例.
.由优质品率较高的种植基地的抽样数据,估计该基地采摘的桔柚中,直径不低于86.78亳米的桔柚在总体中所占的比例.
附:![]() ,
,![]() .
.

若![]() ,则
,则![]() .
.
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com