
| A. | 4 | B. | 1或4 | C. | 2 | D. | 1或2 |
分析 首先求出a2011-a2010=3(s2010-s2009),然后根据前n项和公式化简,即可求出q的值.
解答 解:a2011=3S2010+2012 ①
a2010=3S2009+2012 ②
①-②得:
a2011-a2010=3(s2010-s2009),
∴(q-1)a2010=3×$\frac{{a}_{1}({q}^{2010}-1)-{a}_{1}({q}^{2009}-1)}{q-1}$=3×$\frac{{a}_{1}(q-1){q}^{2009}}{q-1}$,
∴(q-1)a2010=3×a2010,
∴q-1=3,
∴q=4.
故选:A.
点评 本题考查可等比数列的性质和前n项和,关键是求出a2011-a2010=3(s2010-s2009),要注意化简过程要认真仔细,确保正确,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{4}{5}$i | D. | -$\frac{4}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
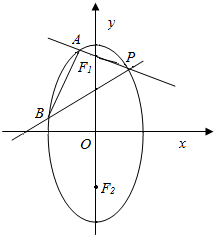 已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)的两个焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,直线$y=\sqrt{2}$过椭圆的焦点,点P是椭圆上位于第一象限的点,并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.
已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)的两个焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,直线$y=\sqrt{2}$过椭圆的焦点,点P是椭圆上位于第一象限的点,并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
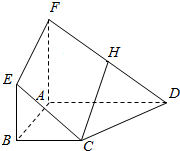 如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.
如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<a | B. | 1<a≤3 | C. | 1<a≤$\frac{5}{2}$ | D. | a≥3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
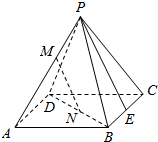 如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.
如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com