
【题目】一士兵要在一个半径为![]() 的圆形区域内检查是否埋有地雷,他所用的检查仪器的有效作用范围的半径为
的圆形区域内检查是否埋有地雷,他所用的检查仪器的有效作用范围的半径为![]() .求该士兵从该圆边界上一点
.求该士兵从该圆边界上一点![]() 出发,至少需走多少米才能将区域检测完,且回到出发点?
出发,至少需走多少米才能将区域检测完,且回到出发点?
【答案】![]()
【解析】
首先,求士兵从![]() 出发,将圆
出发,将圆![]() 的边界上的所有点检测完回到
的边界上的所有点检测完回到![]() 的最短路径
的最短路径![]() .
.
下面用反证法证明:
(1)![]() 上任意两点连线段在
上任意两点连线段在![]() 所围区域内(含边界),即
所围区域内(含边界),即![]() 是凸的;
是凸的;
(2)![]() 与圆
与圆![]() 内部无交点.
内部无交点.
(1)否则,设![]() 、
、![]() ,且线段
,且线段![]() 在
在![]() 所围区域外(如图).
所围区域外(如图).
用线段![]() 代替
代替![]() 中
中![]() 、
、![]() 间的曲线,得到另一条封闭曲线
间的曲线,得到另一条封闭曲线![]() .
.
则曲线![]() 在
在![]() 所围区域内(含边界).
所围区域内(含边界).
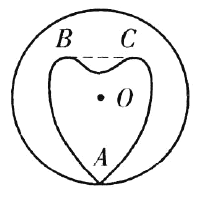
对圆![]() 边界上任一点
边界上任一点![]() ,设士兵在
,设士兵在![]() 上的点
上的点![]() 处检测
处检测![]() ,则
,则![]() .
.
取线段![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() .
.
故士兵沿![]() 也可以将圆
也可以将圆![]() 的边界上所有点检测.
的边界上所有点检测.
但![]() 的长度小于
的长度小于![]() 的长度,矛盾.
的长度,矛盾.
(2)否则,设![]() 、
、![]() ,
,![]() 中
中![]() 、
、![]() 之间的曲线
之间的曲线![]() 在圆
在圆![]() 内部(如图).
内部(如图).
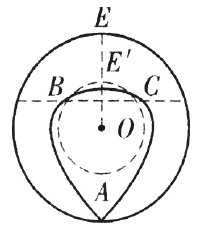
过圆心![]() 作
作![]() 交圆
交圆![]() 于点
于点![]() ,其中,
,其中,![]() 与曲线
与曲线![]() 在直线
在直线![]() 同侧.
同侧.
设线段![]() 与圆
与圆![]() 交于点
交于点![]() .
.
由![]() 的凸性知,曲线
的凸性知,曲线![]() 与
与![]() 的其余部分在直线
的其余部分在直线![]() 两侧.
两侧.
则![]() ,
,
即士兵沿![]() 无法检测点
无法检测点![]() ,矛盾.
,矛盾.
由(1),(2)知![]() 是含点
是含点![]() 且将圆
且将圆![]() 包含在内部的封闭曲线.
包含在内部的封闭曲线.
则![]() 的长度的最小值为
的长度的最小值为![]() (将
(将![]() 想成套在圆
想成套在圆![]() 上的绳子,当从点
上的绳子,当从点![]() 拉紧绳子时,得到绳子的最短长度为
拉紧绳子时,得到绳子的最短长度为![]() ).
).
易证当![]() 时,士兵可沿
时,士兵可沿![]() 将圆
将圆![]() 内所有点检测.
内所有点检测.


科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,椭圆
成等比数列,椭圆![]() 上的点到焦点
上的点到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 过该椭圆的右焦点作两条互相垂直的弦
过该椭圆的右焦点作两条互相垂直的弦![]() 与
与![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生的数学和物理成绩如下:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学成绩 | 80 | 75 | 70 | 65 | 60 |
物理成绩 | 70 | 66 | 68 | 64 | 62 |
(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系的,在上述表格中,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)利用残差分析回归方程的拟合效果,若残差和在![]() 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
(3)现从5名同学中任选两人参加访谈活动,求1号同学没被选中的概率.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: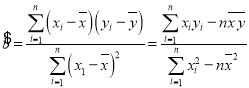 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 的交于
的交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com