
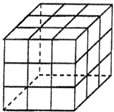
 如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为________.
如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为________.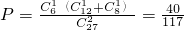
 求出事件的概率,由题设条件可以看出,应先研究出一个面涂有颜色的小正方体的个数以及至少有两个面涂有颜色的小正方体的个数,再计算出事件所包含的基本事件的个数
求出事件的概率,由题设条件可以看出,应先研究出一个面涂有颜色的小正方体的个数以及至少有两个面涂有颜色的小正方体的个数,再计算出事件所包含的基本事件的个数 =
=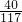
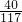


科目:高中数学 来源: 题型:
 如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为
如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为
| ||||||
|
| 40 |
| 117 |
| ||||||
|
| 40 |
| 117 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2006
广州模拟)如图所示,在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱3等分,然后从等分点把正方体锯开,得到27个棱长为1的小正方体,将这小正方体充分混合后,装入一个口袋中.(1)
从这个口袋中任意取出1小正方体,这个小正方体的表面恰好没涂颜色的概率是多少?(2)
从这个口袋中同时任意取出2个小正方体,其中1个小正方体恰好有1个面涂有颜色,另1个小正方体至少有2个面涂有颜色的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)从这个口袋中任意取出1个小正方体,这个小正方体的表面恰好没有颜色的概率为多少?
(2)从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为多少?
查看答案和解析>>
科目:高中数学 来源:2010年河北省石家庄市正定中学高考百日摸底数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com