分析:(1)先寻找直线与平面的所成角,取AB中点H,连接A1H,根据线面所成角的定义可知∠A1AB是A1A与平面ABCD所成的角,在三角形A1AB中求出此角的正切值即可;
(2)先寻找二面角的平面角,取AD中点K,连接D1K,KH,取HK的中点M,取A1D1的中点N,连接MN,AM,AN,根据二面角平面角的定义可知∠MAN就是面AA1D1与面ABCD所成的二面角,然后在三角形MAN中求出此角的余弦值即可.
(3)根据该多面体为长方体削去四个全等的三棱锥,先求出三棱锥的体积,然后利用长方体的体积减去四个全等的三棱锥的体积即可求出所求.
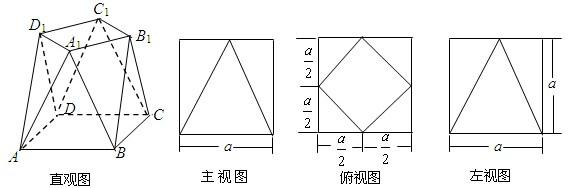
解答:解:(1)由已知图可得,平面A
1AB⊥平面ABCD,取AB中点H,连接A
1H,
在等腰△A
1AB中,有A
1H⊥AB,则A
1H⊥平面ABCD.
∴∠A
1AB是A
1A与平面ABCD所成的角.
∵A
1H=2AH,∴
tan∠A1AB==2.
故A
1A与平面ABCD所成角的正切值为2.
(2)解:取AD中点K,连接D
1K,KH,
同理有D
1K⊥平面ABCD,即△AHK是△AA
1D
1在平面ABCD内的射影.
取HK的中点M,取A
1D
1的中点N,连接MN,AM,AN,
则∠MAN就是面AA
1D
1与面ABCD所成的二面角.
∵MN=a,
AM=a,∴
tan∠MAN==2.即
cos∠MAN=.
∴面AA
1D
1与面ABCD所成二面角的余弦值为
.
(3)∵该多面体为长方体削去四个全等的三棱锥,
每个三棱锥的体积都为
••••a=a3.
∴此多面体的体积
V=a3-4•a3=a3.
点评:本题考查了线面所成角、二面角的度量和多面体的体积等有关知识,体积的求解在最近两年高考中频繁出现,值得重视.



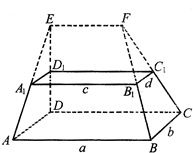 如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h. 已知:右图为一个多面体ABCD-A1B1C1D1的三视图,其中各边长度及位置关系如三视图所表示,
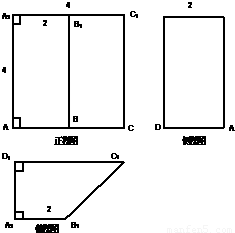
已知:右图为一个多面体ABCD-A1B1C1D1的三视图,其中各边长度及位置关系如三视图所表示, 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.