
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,请根据图象.
轴左侧的图象,如图所示,请根据图象.
(![]() )写出函数
)写出函数![]() 的增区间.
的增区间.
(![]() )写出函数
)写出函数![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() ,求函数
,求函数![]() 的最小值.
的最小值.

科目:高中数学 来源: 题型:
【题目】如果函数![]() 在其定义域内存在实数
在其定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“可拆分函数”.
为“可拆分函数”.
(1)试判断函数![]() 是否为“可拆分函数”?并说明你的理由;
是否为“可拆分函数”?并说明你的理由;
(2)证明:函数![]() 为“可拆分函数”;
为“可拆分函数”;
(3)设函数![]() 为“可拆分函数”,求实数
为“可拆分函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
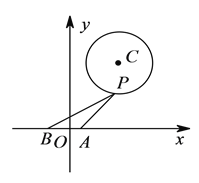
【题目】如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆![]() 的方程为
的方程为![]() ,点
,点![]() 为圆上的动点.
为圆上的动点.
(1)求过点![]() 的圆
的圆![]() 的切线方程.
的切线方程.
(2)求![]() 的最大值及此时对应的点
的最大值及此时对应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若1+ ![]() =
= ![]() .
.
(1)求角A的大小;
(2)若函数f(x)=2sin2(x+ ![]() )﹣
)﹣ ![]() cos2x,x∈[
cos2x,x∈[ ![]() ,
, ![]() ],在x=B处取到最大值a,求△ABC的面积.
],在x=B处取到最大值a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良. 
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良 | 优良(人数) | 非优良(人数) | 合计 |
甲 | |||
乙 | |||
合计 |
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率. 下面的临界值表供参考:
P(x2k) | 0.10 | 0.05 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
(以下临界值及公式仅供参考 ![]() ,n=a+b+c+d)
,n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cosB= ![]() ,tanC=
,tanC= ![]() . (Ⅰ)求tanB和tanA;
. (Ⅰ)求tanB和tanA;
(Ⅱ)若c=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() ,圆O:x2+y2=a2与y轴正半轴交于点B,过点B的直线与椭圆E相切,且与圆O交于另一点A,若∠AOB=60°,则椭圆E的离心率为( )
,圆O:x2+y2=a2与y轴正半轴交于点B,过点B的直线与椭圆E相切,且与圆O交于另一点A,若∠AOB=60°,则椭圆E的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=8,AD=4,AB=2DC=4 ![]() .
. 
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( ) 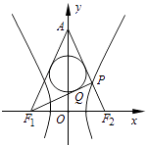
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com