
【题目】经统计分析,我市城区某拥挤路段的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当该路段的车流密度达到180辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为40千米/小时;当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度x为多大时,该拥挤路段车流量(单位时间内通过该路段某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() ,
,![]() 的公共点为
的公共点为![]() .
.
(Ⅰ)求直线![]() 的斜率;
的斜率;
(Ⅱ)若点![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,当
上的动点,当![]() 取最大值时,求四边形
取最大值时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某森林公园有一直角梯形区域ABCD,其四条边均为道路,AD∥BC,∠ADC=90°,AB=5千米,BC=8千米,CD=3千米.现甲、乙两管理员同时从![]() 地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.
地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.

(1)若甲、乙两管理员到达D的时间相差不超过15分钟,求乙的速度v的取值范围;
(2)已知对讲机有效通话的最大距离是5千米.若乙先到达D,且乙从A到D的过程中始终能用对讲机与甲保持有效通话,求乙的速度v的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
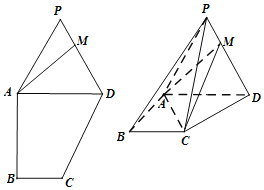
【题目】如图,在多边形PABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,M是线段PD上的一点,且
,M是线段PD上的一点,且![]() ,若将
,若将![]() 沿AD折起,得到几何体
沿AD折起,得到几何体![]() .
.
![]() 证明:
证明:![]() 平面AMC
平面AMC
![]() 若
若![]() ,且平面
,且平面![]() 平面ABCD,求三棱锥
平面ABCD,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨, ![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量, ![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(Ⅰ)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小;
的平均数与中位数的大小;
(Ⅱ)根据直方图估计利润![]() 不少于57万元的概率.
不少于57万元的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com