分析:(Ⅰ)由面面垂直的性质定理得到AB⊥CD,再由A1C=CA,D为AA1的中点得到CD⊥AA1,由线面垂直的判断得到结论;
(Ⅱ)首先证明A1C⊥面ABC,然后以C为原点建立空间直角坐标系,运用平面法向量求解二面角.
解答:(Ⅰ)证明:∵侧面ACC
1A
1⊥面ABC,AB⊥AC,∴AB⊥平面ACC
1A
1,
又CD?面ACC
1A
1∴AB⊥CD,
又A
1C=CA,D为AA
1的中点,∴CD⊥AA
1,
由AB⊥CD,CD⊥AA
1,AB∩AA
1=A,
∴CD⊥平面ABB
1A
1.
(Ⅱ)解:∵AA
1=
a,A
1C=CA=a,∴A
1C⊥AC,又侧面ACC
1A
1⊥面ABC,∴A
1C⊥面ABC
在平面ABC内,过C点作AC的垂线为y轴,AC为x轴,A
1C为z轴建立如图所示空间坐标系.
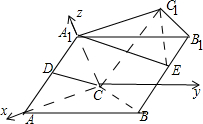
不妨取a=1,其则A(1,0,0),B(1,1,0),A
1(0,0,1),C
1(-1,0,1),B
1(0,1,1)
E
(,1,),
=(-1,0,0);=(,1,-),
设面A
1C
1E的法向量为
=(x,y,z),
由
⇒
,取z=2,得y=1,∴
=(0,1,2),
又面ACA
1C
1法向量为
=(0,1,0),
则二面角的余弦为
cosθ===.
点评:本题考查了直线与平面垂直的判定,考查了用空间向量求二面角的大小,用平面法向量求二面角时,注意法向量所成的角是二面角的平面角还是其补角,此题为中档题.

 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=


 天天向上口算本系列答案
天天向上口算本系列答案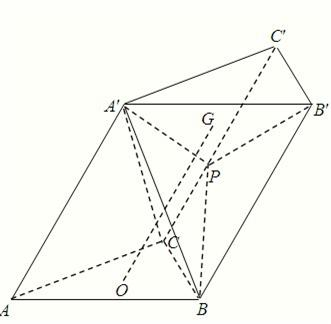 在斜三棱柱ABC-A′B′C′中,底面△ABC为正三角形,设AA′:AC=λ.顶点A′在底面ABC上的射影O是△ABC的中心,P为侧棱CC′中点,G为△PA′B′的重心.
在斜三棱柱ABC-A′B′C′中,底面△ABC为正三角形,设AA′:AC=λ.顶点A′在底面ABC上的射影O是△ABC的中心,P为侧棱CC′中点,G为△PA′B′的重心. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC= 时,求证:平面A′B′P⊥平面BB′C′C;
时,求证:平面A′B′P⊥平面BB′C′C;
 时,求证:平面A′B′P⊥平面BB′C′C;
时,求证:平面A′B′P⊥平面BB′C′C;
 .
.