
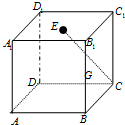
正方形ABCD与正方形ABEF所在平面相交于AB, 在AE、BD上各有一点P、Q, 且AP=DQ.求证: PQ∥平面BCE.
【证明】 法一: .作PM∥AB交BE于M, 作QN∥AB交BC于N, 连接MN.∵正方形ABCD和正方形ABEF有公共边AB, ∴AE=BD.
又AP=DQ, ∴PE=QB,
又PM∥AB∥QN,
∴![]() =
=![]() =
=![]() ,
, ![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PM∥QN,且 PM=QN即四边形PMNQ为平行四边形, ∴PQ∥MN.又MN![]() 平面BCE, PQ
平面BCE, PQ![]() 平面BCE,
平面BCE,
∴PQ∥平面BCE.
法二: , 连接AQ, 并延长交BC的延长线于K, 连接EK, ∵AE=BD, AP=DQ,
∴PE=BQ, ∴![]() =
=![]() ,
,
又AD∥BK,
∴![]() =
=![]() , ∴
, ∴![]() =
=![]() ,
,
∴PQ∥EK.
又PQ ![]() 平面BCE, EK
平面BCE, EK![]() 平面BCE,
平面BCE,
∴PQ∥平面BCE.
法三: , 在平面ABEF内, 过点P作PM∥BE, 交AB于点M, 连接QM.
∴PM∥平面BCE,
又∵平面ABEF∩平面BCE=BE,
∴PM∥BE, ∴![]() =
=![]() , 又AE=BD, AP=DQ, ∴PE=BQ,
, 又AE=BD, AP=DQ, ∴PE=BQ,
∴![]() =
=![]() , ∴
, ∴![]() =
=![]() ,
,
∴MQ∥AD, 又AD∥BC,
∴MQ∥BC, ∴MQ∥平面BCE,
又PM∩MQ=M, ∴平面PMQ∥平面BCE,
又PQ![]() 平面PMQ, ∴PQ∥平面BCE.
平面PMQ, ∴PQ∥平面BCE.


科目:高中数学 来源:2010-2011学年江西省高三习题精编(11) 题型:填空题
己知边长为单位长的正方形ABCD,若A点与坐标原点重合,边AB,AD分别落在x轴, y轴的正方向上,则向量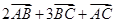 的坐标为
的坐标为
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0条 | B.1条 | C.2条 | D.无数条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com