
| A. | 双曲线的一部分 | B. | 椭圆的一部分 | C. | 直线的一部分 | D. | 无法确定 |
分析 将内切圆的圆心坐标进行转化成圆与横轴切点Q的横坐标,PF1-PF2=F1Q-F2Q=2a,F1Q+F2Q=F1F2解出OQ,可得结论.
解答 解:如图设切点分别为M,N,Q,则△PF1F2的内切圆的圆心的横坐标与Q横坐标相同.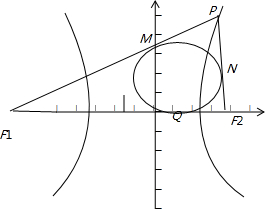
由双曲线的定义,PF1-PF2=2a=4.
由圆的切线性质PF1-PF2=FIM-F2N=F1Q-F2Q=2a,
∵F1Q+F2Q=F1F2=2c,
∴F1Q=a+c,F2Q=c-a,
∴OQ=F1F2-QF2=c-(c-a)=a.
∴△F1PF2内切圆与x轴的切点坐标为(a,0),
∴当P变化时,I的轨迹为直线的一部分.
故选C.
点评 本题巧妙地借助于圆的切线的性质,强调了双曲线的定义.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{21}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{4}=1$ | D. | $\frac{y^2}{25}+\frac{x^2}{21}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | 6 | C. | -6 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com