
【题目】下列类比推理的结论正确的是( )
①类比“实数的乘法运算满足结合律”,得到猜想“向量的数量积运算满足结合律”;
②类比“平面内,同垂直于一直线的两直线相互平行”,得到猜想“空间中,同垂直于一直线的两直线相互平行”;
③类比“设等差数列{an}的前n项和为Sn , 则S4 , S8﹣S4 , S12﹣S8成等差数列”,得到猜想“设等比数列{bn}的前n项积为Tn , 则T4 , ![]() ,
, ![]() 成等比数列”;
成等比数列”;
④类比“设AB为圆的直径,p为圆上任意一点,直线PA,PB的斜率存在,则kPA . kPB为常数”,得到猜想“设AB为椭圆的长轴,p为椭圆上任意一点,直线PA,PB的斜率存在,则kPA . kPB为常数”.
A.①②
B.③④
C.①④
D.②③
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】现有0,1,2,3,4,5六个数字.
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=(﹣x2+ax﹣3)ex(其中a实数,e是自然对数的底数).
(1)当a=5时,求函数y=g(x)在点(1,e)处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)若存在x1 , x2∈[e﹣1 , e](x1≠x2),使方程g(x)=2exf(x)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: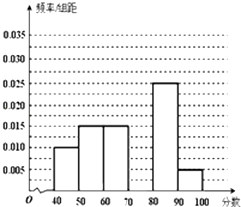
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)用分层抽样的方法在分数段为[60,80)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[70,80)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在多面体SP﹣ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.
(1)求证:AE∥面SPD;
(2)求三棱锥S-BPD的体积。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列![]() 中,
中, ![]() 分别是下表中第
分别是下表中第![]() 行中的某一个数,且
行中的某一个数,且![]() 中任何两个数不在下表的同一列中.
中任何两个数不在下表的同一列中.
第 | 第 | 第 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com