
分析 (1)利用奇函数定义,在f(-x)=-f(x)中的运用特殊值求a,b的值;
(2)根据函数单调性的定义进行证明即可.
(3)结合函数的单调性和奇偶性把不等式f(t2-2t)+f(2t2-k)<0转化为关于t的一元二次不等式,最后由一元二次不等式知识求出k的取值范围.
解答 解:(1)∵定义域为R的函数f(x)=$\frac{a-{2}^{x}}{b+{2}^{x}}$是奇函数,
∴f(0)=0,即f(0)=$\frac{a-1}{b+1}$=0,
即a-1=0,解得a=1,
则f(x)=$\frac{1-{2}^{x}}{b+{2}^{x}}$,
同时f(-x)=-f(x),
即$\frac{1-{2}^{-x}}{b+{2}^{-x}}$=-$\frac{1-{2}^{x}}{b+{2}^{x}}$,
即$\frac{{2}^{x}-1}{b•{2}^{x}+1}$=-$\frac{1-{2}^{x}}{b+{2}^{x}}$,
即1+b•2x=b+2x,
∴b=1;
(2)∵a=b=1,∴f(x)=$\frac{1-{2}^{x}}{1+{2}^{x}}$=$\frac{2-(1+{2}^{x})}{1+{2}^{x}}$=-1+$\frac{2}{1+{2}^{x}}$,
∵2x为增函数,∴f(x)是R上的减函数.
证明:设x1<x2,f(x1)-f(x2)=-1+$\frac{2}{1+{2}^{{x}_{1}}}$-(-1+$\frac{2}{1+{2}^{{x}_{2}}}$)=$\frac{2}{1+{2}^{{x}_{1}}}$-$\frac{2}{1+{2}^{{x}_{2}}}$=$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$(10分)
∵${x_1}<{x_2}∴{2^{x_1}}<{2^{x_2}}$,${2^{x_2}}-{2^{x_1}}>0$
∵${2^{x_1}}+1>0,{2^{x_2}}+1>0$,
∴$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$>0
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)在(-∞,+∞)上是减函数;
(3)∵f(x)是奇函数,
∴f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(k-2t2),
∵f(x)为减函数,由上式可得:t2-2t>k-2t2.
即对一切t∈R有:3t2-2t-k>0,
从而判别式$△=4+12k<0⇒k<-\frac{1}{3}$.
则k的取值范围是k<-$\frac{1}{3}$.
点评 本题主要考查函数奇偶性与单调性的综合应用;同时考查一元二次不等式恒成立问题的解决策略.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{10}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
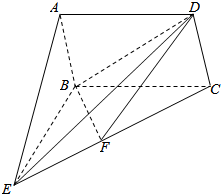 已知矩形ABCD⊥平面BCE,且EB⊥BC,点F是BC的中点,且EB=BC.
已知矩形ABCD⊥平面BCE,且EB⊥BC,点F是BC的中点,且EB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com