
| n |
 |
| k=0 |
| k |
| n |
| P | k n |
| ||
| 1 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | k n |
| 1 |
| 3 |
| 2 |
| 3 |
| n |
 |
| k=0 |
| k |
| n |
| P | k n |
| C | 0 n |
| 0 |
| n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 n |
| 1 |
| n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | r n |
| r |
| n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | n n |
| n |
| n |
| 1 |
| 3 |
| C | r n |
| r |
| n |
| n! |
| r!(n-r)! |
| r |
| n |
| n |
 |
| k=0 |
| k |
| n |
| P | k n |
| C | 0 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | n-1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 0 n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | n-1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:河南省09-10学年高二下学期期末数学试题(理科) 题型:解答题
(本小题满分12分)甲、乙两人进行一种游戏,两人同时随机地喊出杠、虎、鸡、虫,按照
杠打虎、虎吃鸡、鸡吃虫、虫啃杠的原则决定胜负。 (比如甲喊杠的同时,乙若喊虎则乙输,乙若
喊虫则乙赢,乙若喊杠或鸡则不分胜负。) 若两人同时喊出一次后不分胜负则继续喊下去,直到
分出胜负。
(Ⅰ)喊一次甲就获胜的概率是多少?
(Ⅱ)甲在喊不超过三次的情况下就获胜的概率是多少?
.COM
查看答案和解析>>
科目:高中数学 来源:2010年江苏省盐城市高考数学二模试卷(解析版) 题型:解答题
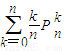 的值.
的值.查看答案和解析>>
科目:高中数学 来源:河南省郑州盛同学校09-10学年高二下学期期末考试理 题型:解答题
甲、乙两人进行一种游戏,两人同时随机地喊出杠、虎、鸡、虫,按照
杠打虎、虎吃鸡、鸡吃虫、虫啃杠的原则决定胜负。 (比如甲喊杠的同时,乙若喊虎则乙输,乙若
喊虫则乙赢,乙若喊杠或鸡则不分胜负。) 若两人同时喊出一次后不分胜负则继续喊下去,直到
分出胜负。
(Ⅰ)喊一次甲就获胜的概率是多少?
(Ⅱ)甲在喊不超过三次的情况下就获胜的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com