
【题目】如图, ![]() ,
, ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,将
的中点,将 ![]() 沿直线
沿直线 ![]() 折起,使二面角
折起,使二面角 ![]() 的大小为
的大小为 ![]() ,则
,则 ![]() 与平面
与平面 ![]() 所成角的正切值是( )
所成角的正切值是( )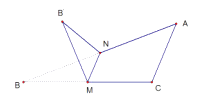
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】∵ ![]() ,AC=BC,M、N分别是BC、AB的中点,
,AC=BC,M、N分别是BC、AB的中点,
将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为 ![]() ,
,
∴∠BMB′为二面角 ![]() 的平面角,即∠BMB′=
的平面角,即∠BMB′= ![]() ,
,
取BM的中点D,连B′D,ND,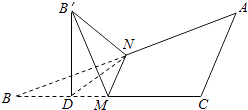
由题意易知:折叠之后平面B′MN与平面BMN所成的二面角即为∠B′MD=60°,
并且B′在底面ACB内的投影点D就在BC上,且恰在BM的中点位置,
∴B′D⊥BC,B′D⊥AD,B′D⊥面ABC,
∴∠B′ND就为斜线B′N与平面ABC所成的角
设AC=BC=t,则B′D= ![]() ,B′N=
,B′N= ![]() ,DN=
,DN= ![]() ,
,
tan∠B′ND= ![]() =
= ![]() .
.
故B'N与平面ABC所成角的正切值是 ![]() .
.
所以答案是:D.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则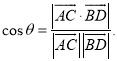 .
.


科目:高中数学 来源: 题型:
【题目】某校高一学生共有500人,为了了解学生的历史学习情况,随机抽取了50名学生,对他们一年来4次考试的历史平均成绩进行统计,得到频率分布直方图如图所示,后三组频数成等比数列.
(1)求第五、六组的频数,补全频率分布直方图;
(2)若每组数据用该组区间中点值(例如区间[70,80)的中点值是
75作为代表,试估计该校高一学生历史成绩的平均分;
(3)估计该校高一学生历史成绩在70~100分范围内的人数.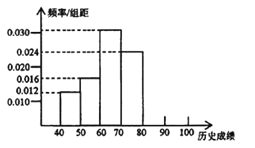
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批产品抽50件测试,其净重介于13克与19克之间,将测试结果按如下方式分成六组:第一组,净重大于等于13克且小于14克;第二组,净重大于等于14克且小于15克;…第六组,净重大于等于18克且小于19克.如图是按上述分组方法得到的频率分布直方图.设净重小于17克的产品数占抽取数的百分比为x,净重大于等于15克且小于17克的产品数为y,则从频率分布直方图中可分析出x和y分别为( )
A.0.9,35
B.0.9,45
C.0.1,35
D.0.1,45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求f(x)的最小正周期和单调递增区间;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对角为x,试求x的范围及此时函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足an= ![]() +2n﹣2,n∈N* , 且S2=6.
+2n﹣2,n∈N* , 且S2=6.
(1)求数列{an}的通项公式;
(2)证明: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 为定义域
为定义域![]() 上的单调函数,且存在区间
上的单调函数,且存在区间![]() (其中
(其中![]() ,使得当
,使得当![]() 时,
时,![]() 的取值范围恰为
的取值范围恰为![]() ,则称函数
,则称函数![]() 是
是![]() 上的正函数,区间
上的正函数,区间![]() 叫做函数的等域区间.
叫做函数的等域区间.
(1)已知![]() 是
是![]() 上的正函数,求
上的正函数,求![]() 的等域区间;
的等域区间;
(2)试探求是否存在![]() ,使得函数
,使得函数![]() 是
是![]() 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足f′(x)+2f(x)= ![]() ,且f(1)=
,且f(1)= ![]() ,则不等式f(lnx)>f(3)的解集为( )
,则不等式f(lnx)>f(3)的解集为( )
A.(﹣∞,e3)
B.(0,e3)
C.(1,e3)
D.(e3 , +∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com