
【题目】已知![]() 分别为
分别为![]() 的三内角A,B,C的对边,其面积
的三内角A,B,C的对边,其面积![]() ,在等差数列
,在等差数列![]() 中,
中,![]() ,公差
,公差![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)运用三角形的面积公式和余弦定理,解得a=b=c=2,由等差数列的通项公式可得an=2n;再由数列的通项与前n和的关系,可得数列{bn}为等比数列,求得bn;
(2)由(1)得![]() ,由此利用错位相减求和法能求出Tn.
,由此利用错位相减求和法能求出Tn.
(1)S![]() acsinB
acsinB![]() ac
ac![]() ,∴ac=4,
,∴ac=4,
又![]() ,
,![]() =
=![]() ,
,
∴![]() ,∴b=2,
,∴b=2,
从而![]() =
=![]()
![]() ∴
∴![]() ,
,
故可得:![]() ,∴
,∴![]() =2+2(n﹣1)=2n;
=2+2(n﹣1)=2n;
∵![]() ,∴当n=1时,
,∴当n=1时,![]() ,
,
当n≥2时,![]() ,
,
两式相减,得![]() ,(n≥2)
,(n≥2)
∴数列{![]() }为等比数列,
}为等比数列,
∴![]() .
.
(2)由(1)得![]() ,
,
∴![]() =
=![]()
![]() +
+![]()
![]() +…+
+…+![]()
![]()
=1×21+2×21+3×21+…+![]() ,
,
∴2![]() =1×22+2×23+3×24+…+n2n+1,
=1×22+2×23+3×24+…+n2n+1,
∴﹣![]() =1×21+(22+23+…+2n)﹣n2n+1,
=1×21+(22+23+…+2n)﹣n2n+1,
即:﹣![]() =(1-n)2n+1-2,
=(1-n)2n+1-2,
∴![]() =(n﹣1)2n+1+2.
=(n﹣1)2n+1+2.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,以椭圆![]() (
(![]() )的右焦点
)的右焦点![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() (其中
(其中![]() 为已知椭圆的半焦距),过椭圆上一点
为已知椭圆的半焦距),过椭圆上一点![]() 作此圆的切线,切点为
作此圆的切线,切点为![]() .
.
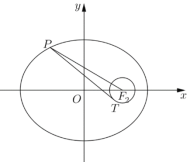
(1)若![]() ,
,![]() 为椭圆的右顶点,求切线长
为椭圆的右顶点,求切线长![]() ;
;
(2)设圆![]() 与
与![]() 轴的右交点为
轴的右交点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() (
(![]() )的直线
)的直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,若
两点,若![]() 恒成立,且
恒成立,且![]() .求:
.求:
(ⅰ)![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 被圆
被圆![]() 所截得弦长的最大值.
所截得弦长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,1,2,2,1,2,4,3,1,2,4,8,4,1,2,4,8,16,5,…,其中第一项是![]() ,第二项是1,接着两项为
,第二项是1,接着两项为![]() ,
,![]() ,接着下一项是2,接着三项是
,接着下一项是2,接着三项是![]() ,
,![]() ,
,![]() ,接着下一项是3,依此类推.记该数列的前
,接着下一项是3,依此类推.记该数列的前![]() 项和为
项和为![]() ,则满足
,则满足![]() 的最小的正整数
的最小的正整数![]() 的值为( )
的值为( )
A.65B.67C.75D.77
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,规定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低![]() 元,根据市场调查,销售商一次订购不会超过600件.
元,根据市场调查,销售商一次订购不会超过600件.
(1)设一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着创新驱动发展战略的不断深入实施,高新技术企业在科技创新和经济发展中的带动作用日益凸显,某能源科学技术开发中心拟投资开发某新型能源产品,估计能获得![]() 万元的投资收益,现准备制定一个对科研课题组的奖励议案:奖金
万元的投资收益,现准备制定一个对科研课题组的奖励议案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,奖金不超过
(单位:万元)的增加而增加,奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .(即:设奖励方案函数模拟为
.(即:设奖励方案函数模拟为![]() 时,则公司对函数模型的基本要求是:当
时,则公司对函数模型的基本要求是:当![]() 时,①
时,①![]() 是增函数;②
是增函数;②![]() 恒成立;③
恒成立;③![]() 恒成立.)
恒成立.)
(1)现有两个奖励函数模型:(I)![]() ;(II)
;(II)![]() .试分析这两个函数模型是否符合公司要求?
.试分析这两个函数模型是否符合公司要求?
(2)已知函数![]() 符合公司奖励方案函数模型要求,求实数
符合公司奖励方案函数模型要求,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD![]() A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
A.不存在B.有且只有两条C.有且只有三条D.有无数条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com