
【题目】已知函数![]()
(1)若函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,
时, ![]()
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:(I)对函数求导,可得函数单调性,并求得函数的最小值,若函数有零点,函数最小值小于零且在定义域范围有函数值大于零,解不等式可得![]() 的范围;(Ⅱ)将
的范围;(Ⅱ)将![]() 代入不等式化简为
代入不等式化简为![]() ,可构造函数
,可构造函数![]()
![]() 利用导数判断单调性可知在
利用导数判断单调性可知在![]() 条件下
条件下![]() 最小值为
最小值为![]() ,
, ![]() 最大值为
最大值为![]() .可证命题.
.可证命题.
试题解析:
(Ⅰ)法1: 函数![]() 的定义域为
的定义域为![]() .
.
由![]() , 得
, 得![]() .
.
因为![]() ,则
,则![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增.
上单调递增.
当![]() 时,
时, ![]() .
.
当![]() 时, 又
时, 又![]() , 则函数
, 则函数![]() 有零点.
有零点.
所以实数![]() 的取值范围为
的取值范围为![]() .
.
法2:函数![]() 的定义域为
的定义域为![]() .
.
由![]() , 得
, 得![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递增, 在
上单调递增, 在![]() 上单调递减.
上单调递减.
故![]() 时, 函数
时, 函数![]() 取得最大值
取得最大值![]() .
.
因而函数![]() 有零点, 则
有零点, 则![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ) 要证明当![]() 时,
时, ![]() ,
,
即证明当![]() 时,
时, ![]() , 即
, 即![]() .
.
令![]() , 则
, 则![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增.
上单调递增.
当![]() 时,
时, ![]() .
.
于是,当![]() 时,
时, ![]() ①
①
令![]() , 则
, 则![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]()
![]() 上单调递增, 在
上单调递增, 在![]() 上单调递减.
上单调递减.
当![]() 时,
时, ![]() .
.
于是, 当![]() 时,
时, ![]() ②
②
显然, 不等式①、②中的等号不能同时成立.
故当![]() 时,
时, ![]() .
.


科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
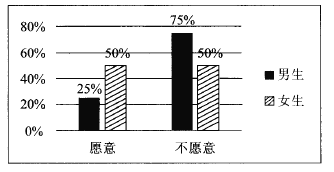
(1)根据条件完成下列![]()
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为![]()
,记甲通过的关数为![]()
,求![]()
的分布列和数学期望.
参考公式与数据:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
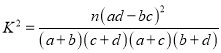
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一医用放射性物质原来质量为a,每年衰减的百分比相同,当衰减一半时,所用时间是10年,根据需要,放射性物质至少要保留原来的,否则需要更换.已知到今年为止,剩余的为原来的![]() ,
,
(1)求每年衰减的百分比;
(2)到今年为止,该放射性物质已衰减了多少年?
(3)今后至多还能用多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一数集的任一元素的倒数仍在该集合中,则称该数集为“可倒数集”.
(1)判断集合A={-1,1,2}是否为可倒数集;
(2)试写出一个含3个元素的可倒数集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: 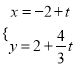 (t为参数),它与曲线C:
(t为参数),它与曲线C: ![]() 相交于A,B两点.
相交于A,B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的![]() ,得曲线C.
,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l: ![]() 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com