


图1 图2
(1)求证:AE⊥BD;
(2)求证:平面PEF⊥平面AECD;
(3)判断DE能否垂直于平面ABC,并说明理由.
(1)证明:连结BD,取AE中点M,连结BM,DM.
∵在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,
∴△ABE与△ADE都是等边三角形.∴BM⊥AE,DM⊥AE.
∵BM∩DM=M,BM,DM?平面BDM,
∴AE⊥平面BDM.
∵BD![]() 平面BDM,∴AE⊥BD.
平面BDM,∴AE⊥BD.
(2)证明:连结CM交EF于点N,连结PN,
∵ME∥FC,且ME=FC,∴四边形MECF是平行四边形.
∴N是线段CM的中点.
∵P是线段BC的中点,∴PN∥BM.
∵BM⊥平面AECD,∴PN⊥平面AECD.
又∵PN![]() 平面PEF,∴平面PEF⊥平面AECD.
平面PEF,∴平面PEF⊥平面AECD.
(3)解:DE与平面ABC不垂直.
证明:假设DE⊥平面ABC,则DE⊥AB,
∴BM⊥平面AECD.∴BM⊥DE.
∵AB∩BM=B,AB,BM![]() 平面ABE,∴DE⊥平面ABE.
平面ABE,∴DE⊥平面ABE.
∴DE⊥AE,这与∠AED=60°矛盾.
∴DE与平面ABC不垂直.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
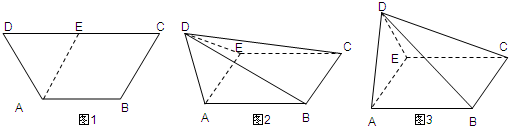 如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.
如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图1,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.将△ABE沿AE折起后如图2,使二面角B-AE-C成直二面角,设F是CD的中点,P是棱BC的中点.
如图1,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.将△ABE沿AE折起后如图2,使二面角B-AE-C成直二面角,设F是CD的中点,P是棱BC的中点.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省上饶市德兴一中高三数学重组卷1(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷10(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com