
【题目】△ABC的内角A,B,C的对边分别为a,b,c.已知asin(A+B)=csin![]() .
.
(1)求A;
(2)求sinBsinC的取值范围;
(3)若△ABC的面积为![]() ,周长为8,求a.
,周长为8,求a.
【答案】(1)A![]() (2)(0,
(2)(0,![]() )(3)a
)(3)a![]()
【解析】
(1)用诱导公式和正弦定理化边为角,然后再由二倍角公式变形后可求得![]() ;
;
(2)由(1)可得![]() ,
,![]() ,把
,把![]() 化为
化为![]() 的函数,由三角函数恒等变换化为一个三角函数形式,结合正弦函数性质可得取值范围;
的函数,由三角函数恒等变换化为一个三角函数形式,结合正弦函数性质可得取值范围;
(3)由三角形面积可求得![]() ,由周长及余弦定理得
,由周长及余弦定理得![]() 的三个等式,消去
的三个等式,消去![]() 可解得
可解得![]() .
.
(1)△ABC中,asin(A+B)=csin![]() ,
,
∴asin(π﹣C)=csin(![]() ),
),
∴asinC=ccos![]() ,由正弦定理得sinAsinC=sinCcos
,由正弦定理得sinAsinC=sinCcos![]() ,
,
∴sinA=cos![]() ,即2sin
,即2sin![]() cos
cos![]() cos
cos![]() ;
;
又A∈(0,π),
∴cos![]() 0,
0,
∴2sin![]() 1,即sin
1,即sin![]() ,
,
∴![]() ,
,
解得A![]() ;
;
(2)∵sinBsinC=sinBsin(![]() B)
B)![]() sinBcosB
sinBcosB![]() sin2B
sin2B![]() sin2B
sin2B![]() cos2B
cos2B![]() sin(2B
sin(2B![]() )
)![]() ,
,
又∵B∈(0,![]() ),
),
∴2B![]() ∈(
∈(![]() ,
,![]() ),sin(2B
),sin(2B![]() )∈(
)∈(![]() ,1],
,1],
∴sinBsinC∈(0,![]() ).
).
(3)△ABC的面积为![]() ,周长为8,
,周长为8,
∴![]() bcsinA
bcsinA![]() bc
bc![]() ,
,
∴bc=4,…①
a+b+c=8,…②
由余弦定理得:a2=b2+c2﹣bc,…③
由①②③组成方程组,可得: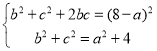 ,
,
可得:(8﹣a)2=a2+12,
解得:a![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.

求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,是一个半圆柱与多面体![]() 构成的几何体,平面
构成的几何体,平面![]() 与半圆柱的下底面共面,且
与半圆柱的下底面共面,且![]() ,
, ![]() 为弧
为弧![]() 上(不与
上(不与![]() 重合)的动点.
重合)的动点.
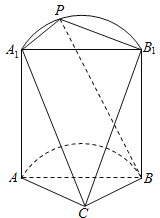
(1)证明: ![]() 平面
平面![]() ;
;
(2)若四边形![]() 为正方形,且
为正方形,且![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形且侧棱垂直与底面的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中,
的组合体中,![]() .
.
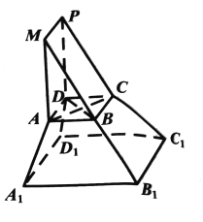
(1)证明:直线![]() 平面
平面![]() ;
;
(2)已知![]() ,且三棱锥A-A1B1D1的体积
,且三棱锥A-A1B1D1的体积![]() ,求该组合体的体积.
,求该组合体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,长轴长为
,长轴长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,求证:由点
,求证:由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() 在(0,+∞)上单调递增,函数g(x)=2x-k.
在(0,+∞)上单调递增,函数g(x)=2x-k.
(1)求m的值;
(2)当x∈[1,2)时,记f(x),g(x)的值域分别为集合A,B,设p:x∈A,q:x∈B,若p是q成立的必要条件,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com