练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在边长为1的等边三角形ABC中，设
    BC
    =2
    BD
    ，
    CA
    =3
    CE

    （1）用向量
    AB
    ，
    AC
    作为基底表示向量
    BE

    （2）求
    AD
    •
    BE
    ．
    分析：（1）根据
    CA
    =3
    CE
    可得
    AE
    =
    2
    3
    AC
    ，再根据
    BE
    =
    BA
    +
    AE
    可用向量
    AB
    ，
    AC
    作为基底表示向量
    BE
    ；
    （2）根据
    AD
    •
    BE
    =
    AD
    （-
    AB
    +
    2
    3
    AC
    ）=
    AD
    •（-
    AB
    ）+
    AD
    •
    2
    3
    AC
    ，然后利用数量积公式可求出所求．
    解答：解：（1）∵
    CA
    =3
    CE

    ∴
    AE
    =
    2
    3
    AC

    ∴
    BE
    =
    BA
    +
    AE
    =-
    AB
    +
    2
    3
    AC
    ------------（4分）
    （2）
    AD
    •
    BE
    =
    AD
    （-
    AB
    +
    2
    3
    AC
    ）=
    AD
    •（-
    AB
    ）+
    AD
    •
    2
    3
    AC
    ---（6分）
    =|
    AD
    |•|
    AB
    |cos150°+
    2
    3
    |
    AD
    |•|
    AC
    |cos30°----------（9分）
    =
    		3
    2
    ×1×(-
    		3
    2
    )    +
    2
    3
    ×
    		3
    2
    ×1×
    		3
    2
    =-
    1
    4
    -----------（12分）
    点评：本题主要考查了平面向量数量积的运算，以及向量的线性表示，同时考查了运算求解的能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    如图，公园内有一块边长为2a的等边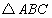形状的三角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．

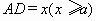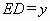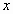    (1)设，，求用表示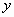的函数关系式．

    (2)如果DE是灌溉水管，为节约成本希望它最短，DE的位置应该在哪里?如果DE是参观路线，则希望它最长，DE的位置又在哪里?请给予证明．

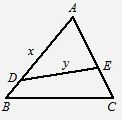
    查看答案和解析>>

    同步练习册答案